Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 123123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Cálculo de Volumes através de Integrais

Considera a região

R = x , y ∈   R 2 : 0 ≤ x ≤ 3 2 , - 1 1 - x 2 ≤ y ≤ 1 1 - x 2

b ) Determine o volume do sólido obtido pela rotação da região R em torno do eixo 0 y .

Passo 1

Vou redesenhar a mesma região que descobrimos na última questão:

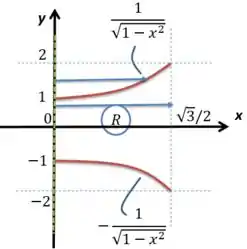
Repara que o eixo agora é o 0 y , que é basicamente o próprio eixo y . Repara que, em primeiro lugar, a figura que vamos rotacionar é simétrica em relação ao eixo x . Vamos dizer então que ela será duas vezes a parte positiva de R rotacionada em torno de y . Nota o seguinte, o raio maior será sempre 3 / 2 e vale de y = 0 até y = 2 . O raio menor vai variar de 1 até 2 , com raio igual à inversa da função y = 1 1 - x 2   , ou seja, x ( y ) dada essa relação; nós invertemos o eixo de rotação, para isso devemos inverter a função igualmente:

y 2 = 1 1 - x 2 → 1 - x 2 = 1 y 2

→ x 2 = 1 - 1 y 2 → x = 1 - 1 y 2

Ok, então o volume ficará, lembrando que temos que dobrá-lo por estar fazendo ele simetricamente em relação ao eixo x , assim:

V = ∫ 0 2 π 3 2 2 d y - ∫ 1 2 π 1 - 1 y 2 2 d y

= ∫ 0 2 π 3 4 d y - ∫ 1 2 π 1 - 1 y 2 d y

π 3 y 4 [ 2 0 - π y + 1 y [ 2 1

= π 3 2 4 + 2 + 1 2 - 1 + 1 1

= π 3 2 + 5 2 - 2

= 2 π

É isso!

Resposta

V = 2 π       u n i d a d e s   d e   v o l .

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .