Considere a região plana definida por:
Seja o sólido de revolução obtido pela rotação de em torno do eixo .
- Esboce a região plana
- Utilizando o método que preferir, escreva o volume de como uma integral
- Calcule o volume de
Passo 1
A questão é sobre sólidos de revolução, mas antes de sabermos como será esse sólido, temos que saber a cara da região que vamos rotacionar pra gera-lo, beleza? Dá uma olhada nessa função:
Essa é a cara de um polinômio de segundo grau. É como se fosse um copo. Os diferentes polinômios de segundo grau vão ser copos também, cada um um pouco diferente do outro. Beleza, mas e daí? Bem, vamos ver de novo a região :
Abrindo o termo :
Opa, está entre dois polinômios de segundo grau! Então vamos achar a cara desses copos! A começar por:
Veja bem, esse “copo” também tem sinal positivo multiplicando o termo , então ele vai ser também um copo pra cima! Mas o que os temos fazem? Vamos ver primeiro se o ponto de mínimo vai se deslocar. Derivando e igualando à , temos:
E quando , temos:
Beleza, então a curva é um copo de boca pra cima com ponto de mínimo . Bora ver a outra curva:
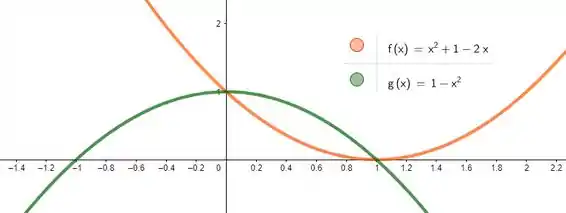
Essa é mais tranquila de entender. Como temos um multiplicando , trata-se de um copo com a boca pra baixo. E como temos um termo , basta a gente pegar , espelhar em relação ao eixo e subir uma unidade com ele. Juntando as duas curvas, temos:
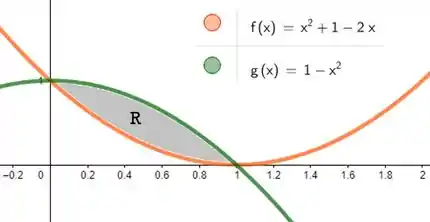
E veja só! Como está entre essas duas curvas, nossa região vai ser ninguém menos do que:
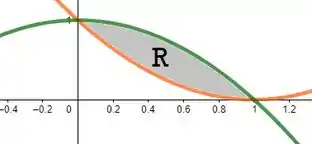
E pra fechar esse passo, vamos só ver antes em que pontos que essas curvas se encontram. Pra calcular o volume depois vai ser interessante. Como as curvas são:
Se igualarmos as duas:
As possíveis soluções vão ser:
O que resulta em:
Substituindo esses valores de na expressão de qualquer uma das duas curvas, achamos os pontos de interseção das curvas:
Os pontos vão ser:
Ok, o gráfico do Geogebra mei oque deu um Spoiler, mas não deixe de achar esses pontos assim viu?
Passo 2
Beleza, agora que sabemos tudo sobre a regiaõ , vamos tentar achar . Pelo método dos discos, que já calcula o volume de revolução em relação ao eixo , temos:

Beleza, mas a nossa região não é bem uma função só rotacionada, e sim duas. Mas não se acanhe, porque se entendermos como a região menos a região :
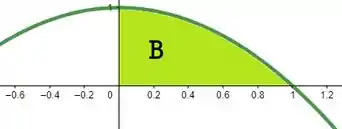
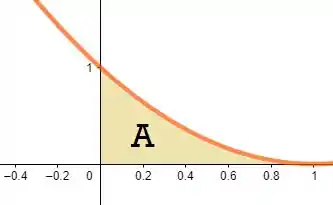
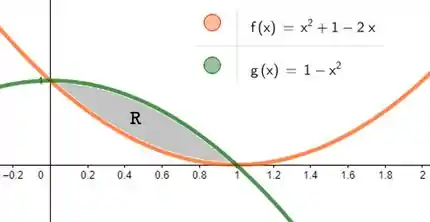
Então o volume de revolução de nada mais vai ser do que o volume de revolução de menos o volume de revolução de . Pra região usaremos então e para a região usaremos então e os limites de integração dos dois vai ser e porque são nesses valores que as curvas se cruzam! Podemos então finalmente montar a equação do volume:
Passo 3
Agora é mão na massa, temos que calcular as integrais:
Na primeira, vamos abrir o quadrado e ficar com:
Realizando a integração:
Na segunda integral, se fizermos a seguinte substituição simples:
Vamos ter:
Realizando a integração:
Se o volume é:
Então calculamos e fechamos a questão: