Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 501234567891011121314151617181920212223242526272829303132333435363738394041424344454647484951525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

3) Considere a região Ω do plano delimitada superiormente por y = cos ⁡ x e inferiormente pelo segmento de reta conectando os pontos do plano - π / 2 ,   0 e π / 2 ,   0 . O volume do sólido obtido girando a região Ω em torno do eixo x é:

  1. π 2 2
  2. π 2 5
  3. π 2 4
  4. π 2 3

Passo 1

Bem, a primeira coisa aqui é desenhar a região Ω ... É a região que está abaixo da cossenoide y = cos ⁡ x ...

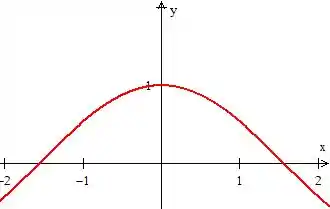
Mas está delimitada pelo segmento de reta que passa pelos pontos - π / 2 ,   0 e π / 2 ,   0 (O segmento está em cima do eixo x )...

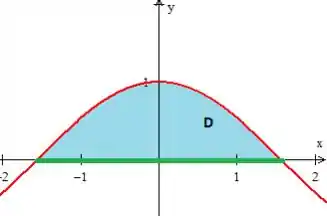
Eis a região Ω !

Passo 2

Quando giramos essa região Ω ao redor do eixo x , obtemos um volumesinho. Para calcular o volume desse sólido, vamos usar a expressão do cálculo do volume pelo método dos discos (pois estamos girando ao redor de x ) :

V = ∫ a b π f x 2 d x

Onde a e b são os limites do sólido em x , ou seja, a é onde começa, no - π / 2 , e b onde termina, no π / 2 nesse caso...

V = ∫ - π / 2 π / 2 π f x 2 d x

A função f é a função do qual estamos calculando o volume girado ao redor de x ...

f x = y = cos ⁡ x

Passo 3

Então, basta calcular essa integral...

V = ∫ - π 2 π 2 π cos ⁡ x 2 d x =

π ∫ - π 2 π 2 cos 2 ⁡ x d x

Para fazer isso, lembremo-nos que

cos 2 ⁡ x = 1 + cos ⁡ 2 x 2

V = π ∫ - π 2 π 2 1 2 + cos ⁡ 2 x 2 d x =

π 1 2 x + 1 2 ⋅ sin ⁡ 2 x 2 - π 2 π 2 =

π 1 2 π 2 + 1 2 ⋅ sin ⁡ π 2 - 1 2 - π 2 + 1 2 ⋅ sin ⁡ - π 2 =

π π 2 = π 2 2

Resposta

  1. π 2 2

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .