Determine o volume do sólido limitado pelos cilindros e .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para determinar o volume de um sólido que é limitado por dois cilindros:
E
Graficamente, temos:
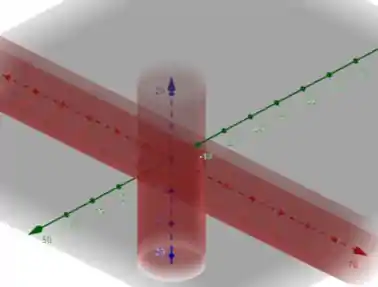
Para isso, podemos calcular o volume pela seguinte integral dupla:
Onde essa multiplicação por significa que vamos utilizar a simetria do sistema para resolver a integral, considerando apenas o eixo positivo de .
Não entendeu? Então bora junto 😉
Passo 2
Bom... como , isolamos na seguinte expressão:
Já para a região de integração do sólido, consideramos o outro cilindro da seguinte forma:
Dessa forma, quando varia de a , então varia da seguinte forma:
Passo 3
Bom... substituindo as expressões e limites na integral, temos:
Entendeu direitinho? Responde aee ;)
