UTFPR– Cálculo Diferencial e Integral II – AVA2 – Questão 2
Determine o volume do sólido limitado por e pelos planos
Passo 1
Oi, tudo bem? Essa questão fala de volume de um sólido! Nosso sólido é delimitado por cima pela função :
E embaixo pelo plano
Beleza?
E no plano ? Ele é delimitado pelo eixo coordenado
E pelas retas
E
e agora, como resolver isso? Por onde começar? Nossa pergunta de milhões...
Vamos esboçar essa região no plano para poder achar nossos limites de integração e poder montar certinho nossa integral!
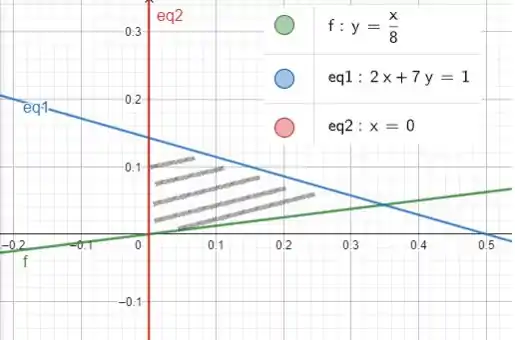
Belezinha até aqui?
A região que compreende as três retas é aquele triângulo deitado mais a esquerda! Essa região é limitada superiormente pela reta azul
E inferiormente pela reta em verde
Então
É onde
Bora resolver?
Então nosso limite em é
E nossa integral fica assim
beleza?
Agora é #partiu integrar!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Nossa integral é a seguinte
Vamos começar resolvendo a mais de dentro (considerando como constante):
E aplicando nos limites de integração em :
Tranquilo?
Vamos guardar esse resultado!
Passo 3
Bora substituir o resultado que guardamos na integral mais de dentro!
A maior parte desses termos a gente vai integrar usando a regra da potência, mas aquele vou usar substituição simples (para não ter que abrir o produto notável)
Agora integrando o restante e juntando esse resultado temos
Beleza? Nossa missão final é aplicar nos limites de integração!
Passo 4
Aplicando os limites em temos
No limite superior:
E no inferior (com sinal negativo, não esqueça):
Juntando os resultados temos:
Ufa, terminamos galera! Vamos para a próxima?