Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 125123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Cálculo de Volumes através de Integrais

Determine o volume do sólido obtido pela revolução em torno do eixo- x , da região limitada pelo gráfico de f x = x 2 e g x = 2 - x 2 no intervalo x   ∈ [ - 1,1 ] .

Passo 1

Vamos começar desenhando essa região, sendo que uma parábola tem boca para cima e seu vértice na origem e a outra tem boca para baixo e vértice em ( 0,2 ) :

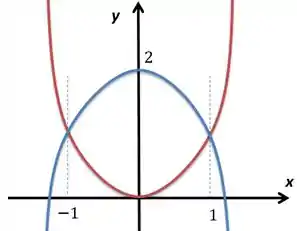
Eu aproveitei e já marquei o intervalo de x bem onde as parábolas se encontram, repara aqui:

f x = g x → x 2 = 2 - x 2

2 x 2 = 2

x 2 = 1

x = ± 1

Legal até aí.

Passo 2

Agora a questão é ver como faremos essa diferença de rotações. Repara que na região delimitada em relação ao eixo de rotação, que é o eixo x , a que está mais afastada é a parábola azul, ou seja, g x = 2 - x 2 . A mais próxima é a vermelha, f x = x 2 . Resumindo a brincadeira, vamos fazer a diferença da rotação da mais externa com a mais interna. Ficará assim, usando a fórmula de seções transversais:

V = ∫ - 1 1 π g x 2 d x - ∫ - 1 1 π f x 2 d x

= ∫ - 1 1 π [ 2 - x 2 2 - x 2 2 ] d x

= ∫ - 1 1 π 4 - 4 x 2 d x

= π 4 x - 4 x 3 3 [ 1 - 1

= π 4 1 - 4 1 3 3 - 4 - 1 - 4 - 1 3 3

= π 4 - 4 3 + 4 - 4 3

= π 16 3

= 16 π 3

Resposta

V = 16 π 3

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .