UFCG – Sem Campus – Cálculo Diferencial e Integral II – Listas de Cálculo 2 – UAMat – Lista 3 – Questão 6a
Determine o volume do sólido obtido com a rotação de cada região em torno do eixo :
A região delimitada pelo triângulo de vértices em e .
Passo 1
Faaaala povo bonito, tudo na paz?
Nessa questão precisamos determinar o volume do sólido obtido quando rotacionamos, em torno do eixo , o triângulo de vértices:
Tranquilo?
Massa! Precisamos escolher algum dos métodos de cálculo de volume de sólido de revolução para aplicar aqui. Vocês têm alguma sugestão?
Como estamos falando de rotação em torno do eixo , um método que facilitará um pouco o nosso trabalho algébrico é o método das cascas. Segundo ele:
Ueee! Que é esse que vamos usar aqui? Como estamos falando de uma região triangular, podemos pensar que não tem envolvido.
Maaaaaass, o triângulo é formado por arestas, e cada uma dessas arestas é como uma reta de equação , sacaram? O método das cascas nos dá o volume de toda a região abaixo da curva .
Assim, o nosso primeiro passo é determinar a equação dessas retas. Lembrando que, se conhecemos dois pontos de uma reta, sua equação é dada por:
Então, bora lá!
Passo 2
Podemos esboçar a nossa região triangular pelos seus vértices:
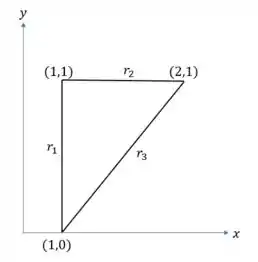
Show de bola!
Agora, vamos identificar a equação das retas que compõem os lados do nosso triângulo.
Começando por ela é simplesmente uma reta vertical, em que sempre vale . Ou seja, a equação dessa reta é:
Legal de observar que, por ser uma reta vertical, nem existe região abaixo dela. Ou seja, quando rotacionarmos esse triângulo, não precisamos nem considerar essa reta na expressão do método das cascas.
Indo agora para , temos uma reta horizontal. Ou seja, nela sempre vale . Logo, sua equação é:
Ela possui região abaixo dela e será considerada no método das cascas.
Por fim, temos uma reta inclinada. Usando a expressão que comentamos no passo :
E usando os dois vértices pertencentes a esse lado:
Vamos ter:
Logo:
Assim, temos para :
Tranquilo até aqui? Vamos prosseguir!
Passo 3
Agora que já conhecemos as equações, e sabemos que apenas e irão contribuir no método das cascas para o cálculo do volume de rotação, podemos montar as integrais.
O volume do triângulo rotacionado deverá ser igual a:
: Volume obtido pela rotação da região abaixo da reta .
Volume obtido pela rotação da região abaixo da reta .
Assim, como pelo método das cascas:
Tomando os limites de integração pelo intervalo em de cada segmento de reta, temos para :
Já para :
Perfeito!
Passo 4
Como já montamos as integrais, vamos calculá-las. Começando por :
Colocando as constantes para fora da integral:
Substituindo os limites de integração:
Vamos para o cálculo de :
Colocando as constantes para fora, temos:
Logo:
Assim:
Agora é só substituir na expressão para e correr pro abraço:
Uhuuuul! É isso, terminamos. Até a próxima gente 😊