UFCG – Sem Campus – Cálculo Diferencial e Integral II – Listas de Cálculo 2 – UAMat – Lista 3 – Questão 7
Determine o volume do sólido obtido pela rotação da região, no primeiro quadrante, limitada superiormente pela curva , inferiormente pelo eixo e à direita pela reta , em torno da reta
Passo 1
Faaaaaaala galera, tudo certo com vocês?
Bora resolver mais uma questãozinha de cálculo!!
Aqui precisamos calcular o volume de um sólido de revolução.
Ele é obtido pela rotação da região, no primeiro quadrante, limitada pelas curvas:
em torno da reta .
Puts, então dessa vez não estamos rotacionando em torno do eixo ou , mas em torno da reta . Será que isso muda muita coisa? Ainda podemos aplicar os mesmos métodos de antes?
Então galera, muda algumas coisas sim.
Para calcular volume de sólidos de revolução, podemos usar o método das cascas, segundo ele:
Porém, essa expressão é válida quando rotacionamos em torno do eixo . Como aqui iremos rotacionar em torno do eixo , precisamos ajustar o termo que representa a distância até o eixo de rotação. Assim:
Massa! Então, vamos entender melhor qual é a nossa região que será rotacionada, para depois montarmos a integral, beleza?
Passo 2
Vamos começar identificando a nossa região que será rotacionada. Ela é delimitada pelas curvas:
A primeira curva é uma parábola, com vértice em . Como estamos considerando a região apenas no quadrante, temos:
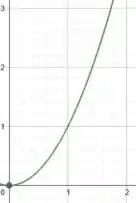
Show! Analisando as outras duas curvas, temos algo um pouco mais simples.
é o próprio eixo .
é a reta vertical que passa por .
Assim, colocando tudo em um mesmo gráfico:
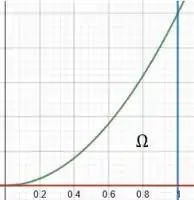
Uhuuul! Encontramos a nossa região que será rotacionada.
Passo 3
Bom, já que identificamos a nossa região , vamos buscar montar a integral pelo método das cascas. Já vimos que:
Como, no caso de , essa região está abaixo da curva , no intervalo de a , podemos escrever que:
Colocando as constantes para fora, ficamos com:
Usando a regrinha de integração de polinômios:
Ficamos com: