UFCG. Cálculo Diferencial e Integral II. Listas de Cálculo 2 UAMat. Lista 3. Questão 2a.
2 - Determine o volume do sólido obtido com a rotação da região sombreada em torno do eixo :
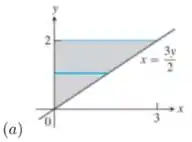
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nosso objetivo aqui nesse problema é obter o volume do sólido que se forma ao rotacionar a área hachurada em torno do eixo .
Como podemos obter esse volume? 🤔
Nesse caso, podemos usar o método dos discos em que usamos a ideia do cálculo do volume de um disco para obter o volume do nosso sólido.
A fórmula do volume de um disco é
E como nosso sólido não é um disco, vamos obter o volume de altura infinitesimal de cada disco.
Portanto, na verdade é uma altura infinitesimal e é um volume infinitesimal.
Tranquilo até aqui? 😁
Passo 2
Se o eixo de rotação é o eixo , a função será o raio de cada disco! Ou seja
Integrando nos dois lados, chegamos em
Como queremos apenas o intervalo de altura em entre e , aplicamos esse limite como os limites de integração.
Como e , então
Como é uma constante, podemos tirá-la da integral.
Interessante, não é? 😉
Passo 3
Integrando pelo método de integração polinomial, somando no expoente de e a dividindo pelo resultado da soma do seu expoente, temos
Aplicando os limites de integração, chegamos em
Substituindo em , temos
Simplificando...
Então chegamos à conclusão que o volume do solido de revolução é ! Legal, não é? 😎
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
