UFCG. Cálculo Diferencial e Integral II. Listas de Cálculo 2 UAMat. Lista 3. Questão 1a.
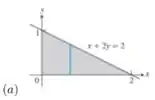
1 - Determine o volume do sólido obtido com a rotação da região sombreada em torno do eixo :
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema queremos obter o volume do sólido de revolução da reta em torno do eixo com variando entre e .
Temos alguns métodos para obter esse volume, tem algum em mente para esse caso? 🤔
Ao rotacionarmos a figura do enunciado em torno do eixo , podemos perceber que o solido que se forma é um cone. Assim podemos usar a fórmula do volume do cone pois, pela figura, o raio da base é e a altura é . Mas qual seria a graça de fazer por esse modo?
Portanto vamos usar o método dos discos.
A volume do disco é dado por
Onde é o raio e é a altura.
O método dos discos consiste em calcular cada volume dos discos infinitesimais que formam o nosso sólido.
Assim perceba que é o mesmo que e é o mesmo que .
Entendeu? Vamos aplicar esse método!
Passo 2
Substituindo e em , vemos que cada volume infinitesimal é dado por
Integrando dos dois lados, chegamos em
A altura do nosso solido é dado por , então temos que integrar dentro do intervalo que nosso solido está incluído, eu seja, entre e como vemos na imagem do enunciado.
Mas tem mais uma coisa! Foi nos dado uma equação, não uma função de , então temos que manipular essa equação de modo que tenhamos uma função de .
Entendeu? 👀
Passo 3
A equação que nos deram é:
Vamos isolar em um lado.
Agora, fazendo , temos
Substituindo na nossa integral...
Vamos reescrever na forma polinomial e tirar para fora, já que é uma constante
Integrando pelo método de integração polinomial somando no expoente de e dividindo pela soma do expoente, temos
Aplicando os limites de integração...
Substituindo em , vamos obter
Então vemos que o volume do solido formado pela rotação da região sombreada é .
A efeito de comparação, a fórmula do volume do cone é dado por
Se o raio da base e a altura é igual a , então vamos chegar no mesmo resultado!
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
