Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 165123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFCG. Cálculo Diferencial e Integral II. Listas de Cálculo 2 UAMat. Lista 3. Questão 1b.

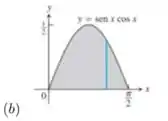
1 - Determine o volume do sólido obtido com a rotação da região sombreada em torno do eixo x :

Passo 1

Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nesse problema, nosso objetivo é calcular o volume do sólido que se forma ao rotacionar a área hachurada na imagem do enunciado em torno do eixo x . Perceba que a área hachurada é limitada pela curva y = s e n x cos ⁡ x e dentro do intervalo de x entre 0 e π / 2 .

Mas como podemos obter esse volume, tem alguma ideia? 🤔🤔

Nesse caso, podemos utilizar o método dos discos. Esse método consiste em calcular o somatório dos volumes infinitesimais de discos que formam nosso solido.

O volume de um disco é dado por

V = π r 2 h

Onde r é o raio do disco e h é a altura.

Estamos interessados no volume infinitesimal de cada disco, ou seja, o volume d V de cada altura d x . Substituindo V por d V e h por d x , temos

d V = π r 2 d x

Entendeu até aqui? 👀

Passo 2

Mas qual é o raio r formado em cada disco de altura d x ? Não é o valor de y ? Ou seja

r = y =   s e n x cos ⁡ x

Substituindo em d V

d V = π s e n x cos ⁡ x 2 d x

Integrando dos dois lados

∫ d V = ∫ π s e n x cos ⁡ x 2 d x

V = ∫ π s e n x cos ⁡ x 2 d x

Queremos o volume dentro do intervalo de x entre 0 e π / 2 , então aplicamos esse intervalo como limites de integração

V = ∫ 0 π / 2 π s e n x cos ⁡ x 2 d x

Com a · b c = a c b c , então

V = ∫ 0 π / 2 π s e n 2 x cos 2 ⁡ x d x

Reescrevendo a função de integração usando identidades trigonométricas, chegamos em

s e n 2 x cos 2 ⁡ x = 1 - cos ⁡ 4 x 8

Substituindo na integral

V = ∫ 0 π / 2 π 1 - cos ⁡ 4 x 8 d x

Como π 8 é uma constante, podemos colocá-lo para fora da integral

V = π 8 ∫ 0 π / 2 1 - cos ⁡ 4 x d x = π 8 ∫ 0 π 2 1 d x - ∫ 0 π 2 cos ⁡ 4 x d x

Agora resolvemos cada integral separadamente e depois substituímos em V .

Sacou? Bora lá! 😎

Passo 3

Primeiro resolvendo a integral

∫ 0 π 2 1 d x

Como a função de integração é uma constante, a integral de uma constante é igual a própria constante multiplicada pela variável de integração

∫ 1 d x = x

Aplicando os limites de integração

∫ 0 π 2 1 d x = x ​ x = 0 π 2 = π 2 - 0

∫ 0 π 2 1 d x = π 2

Agora para a integral

∫ 0 π 2 cos ⁡ 4 x d x

Vamos fazer uma mudança de variáveis e chamar 4 x de u , assim, derivando u com relação a x , temos

d u d x = d 4 x d x = 4 x 1 - 1

d u d x = 4

Isolando d x em um lado da equação, vamos obter

d x = d u 4

Reescrevendo os limites de integração, tínhamos que x variava de 0 a π / 2 , agora em u , temos que u varia entre

u 1 = 4 x = 4 π 2 = 2 π

u 2 = 4 x = 4 · 0 = 0

Substituindo u 1 e u 2 nos limites de integração, 4 x por u e d x por d u / 4 , vamos obter

∫ 0 π 2 cos ⁡ 4 x d x → ∫ 0 2 π cos ⁡ u d u 4

Entendeu o que fizemos? 😉

Passo 4

Tirando a constante 1 / 4 para fora da integral, temos

1 4 ∫ 0 2 π cos ⁡ u d u

Pelo teorema fundamental do cálculo, temos que a integral do cos ⁡ u é igual a s e n u .

1 4 ∫ cos ⁡ u d u = 1 4 s e n u

Aplicando os limites de integração...

1 4 ∫ 0 2 π cos ⁡ u d u = 1 4 s e n u u = 0 2 π

1 4 ∫ 0 2 π cos ⁡ u d u = 1 4 s e n 2 π - 1 4 s e n 0

Como s e n 2 π é igual ao s e n 0 , então

1 4 ∫ 0 2 π cos ⁡ u d u = 0

∫ 0 π 2 cos ⁡ 4 x d x = 0

Substituindo em V , temos

V = π 8 ∫ 0 π 2 1 d x - ∫ 0 π 2 cos ⁡ 4 x d x

V = π 8 π 2 - 0

V = π 2 16

Portanto, o volume de revolução do nosso solido é dado por π 2 16 !

Legal, não é? 🤩

É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta

V = π 2 16

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .