UFCG – Sem Campus – Cálculo Diferencial e Integral II – Listas de Cálculo 2 – UAMat – Lista 3 – Questão 5b
Determine o volume do sólido obtido com a rotação, em torno do eixo , das regiões limitadas pelas retas e curvas:
b) ,
Passo 1
Faaaala galerinha, tudo bom com vocês? Bora matar mais uma questãozinha de Cálculo !
Nesse exercício, basicamente temos uma região no plano e vamos rotacioná-la em torno do eixo . Após efetuar a rotação, teremos um sólido. O enunciado nos pede pra determinar o volume desse sólido, beleza?
Antes de tudo, precisaremos analisar qual a região que será rotacionada. Segundo o enunciado, ela está limitada pelas curvas:
Ok! Depois de identificarmos a região precisaremos calcular, efetivamente, o volume desse sólido de revolução. Vocês lembram como podemos fazer isso?
Temos que usar algum dos nossos métodos para cálculo de sólido revolução. Um que pode ser interessante é o método dos discos, segundo ele:
Show de bola! Então vamos lá 😊
Passo 2
Pra começar, vamos identificar a nossa região do plano que será rotacionada. Como falamos no passo , ela é limitada por curvas:
Começando por , temos a seguinte curva:
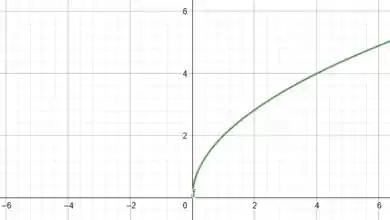
Massa! Ela vale , quando . E, tende pro , quando .
Vamos agora analisar as outras duas curvas. Elas são um pouco mais simples, pois são retas de valores constantes:
É o próprio eixo . E:
Que é a reta constante que passa por . Assim, colocando tudo em um mesmo gráfico, temos:
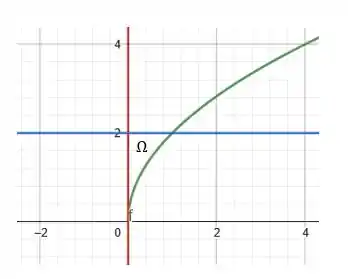
Prontinho, a região determinada é justamente , destacado na figura. Conseguiu entender?
Vamo simbora!
Passo 3
Agora que já identificamos a região, vamos calcular o volume do sólido de revolução.
Pelo método dos discos que comentamos no passo , o volume do sólido de revolução gerado pela rotação da região abaixo da curva , em torno do eixo , é:
Mas, o problema aqui, é que a nossa região não está abaixo da curva , e sim acima dela. O que podemos fazer nesse caso? Alguma ideia?
Então, sabe essa expressão “” que aparece dentro da integral do método dos discos? Ela representa um volume de um disco com raio e espessura :
Assim, pra calcular o volume obtido pela rotação de podemos entendê-lo como a subtração dos volumes de dois discos:
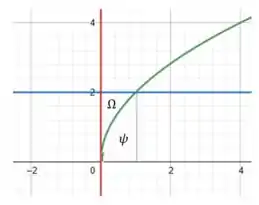
Volume obtido pela rotação da região representada pela união de e , ou seja, região abaixo da reta .
Volume obtido pela rotação da região , ou seja, região abaixo da curva .
Massa!
Pra montarmos nossas integrais, falta apenas definirmos os limites de integração. Trata-se justamente do intervalo em , que nossa região ocupa.
Pela imagem, vemos que o limite inferior ocorre em . Mas, o limite superior ocorre na intersecção de e . Assim:
Excelente! Pelo método dos discos (não esquece essa fórmula hein galera!):
Podemos então montar a integral:
Passo 4
Já tamo acabando! Falta só calcularmos as integrais. Começando por:
Colocando tudo que é constante pra fora da integral, temos:
Boa! A primeira integral já foi. Falta a segunda:
Colocando novamente tudo que é constante para fora da integral, e lembrando que , vem:
Daí é só substituir os limites:
Resumindo, encontramos que:
Lembrando que:
Temos:
Uhuuul! Terminamos. Espero que vocês tenham entendido tudinho. Até a próxima gente 😊