UFCG, Sem Campus, Cálculo Diferencial e Integral II, 1º Estágio - 2022.1, Questão 4
Determine o volume do sólido de revolução obtido pela rotação, em torno do eixo , da região plana delimitada pelas curvas e , com .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular o volume de rotação da região entre as curvas e . Mas como a gente faz isso?
Bom, existem vários métodos pra gente calcular esse volume de rotação, mas a gente tem que prestar atenção em alguns detalhes que pode facilitar nossas contas. No nosso caso, nossa região está girando em torno do eixo e ela é composta por funções de . Então, um método mais simples de calcular o volume, nesse caso, seria através do Método das Cascas Cilíndricas.
Nesse método, a gente considera que o volume é calculado através do produto entre a circunferência, altura e espessura de pedaços infinitesimais de volume do sólido. E a gente usa a integral para “somar” esses produtos infinitesimais. Então, teremos:
Onde representa a circunferência da casca, representa a altura (que no nosso caso é dada pela diferença entre as duas funções dadas) e sua espessura. Vamos usar os dados da questão para substituir os parâmetros da integral e obter o volume.
Vamos lá!
Passo 2
Vamos começar dando uma olhada no gráfico da nossa região:
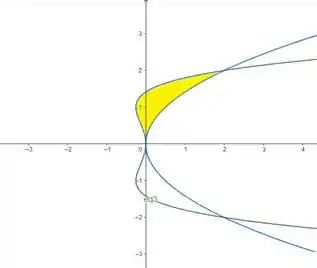
Como o enunciado nos diz que tá variando de a , pra gente só interessa essa partezinha em amarelo. É ela que vai rotacionar em torno do eixo .
A altura da nossa casca vai ser dada pela diferença entre as funções (em verde) e (em azul). Substituindo isso na integral do volume, temos:
Simplificando dentro dos parênteses:
Passo 3
Agora vamos integrar em relação a , usando a regrinha do expoente ():
Aplicando os limites de integração:
Assim, temos nosso volume:
Valeu, galera! Até a próxima! 😉