UFBA, Sem Campus, Cálculo B, Listas de Cálculo B - UFBA - Lista 1, Questão 2.1a
Determine o volume do sólido tal que:
A base de é um círculo de raio , e as seções transversais perpendiculares à um eixo da base são quadrados.
Passo 1
E aí genteee, como é que vocês estão?
Nessa questão temos um sólido meio diferenciado. Basicamente, ele possui uma base circular de raio , mas as suas seções transversais são quadradas.
Assim, o lado dessa seção quadrada que está na base, deve possuir o mesmo comprimento da altura dessa seção. Sei que é bem complicadinho de visualizar, e até de desenhar esse sólido, mas não precisa se preocupar tanto com essa parte.
O mais importante é entendermos como calcular o volume dele 😊
Para fazer isso, vamos usar o método das seções transversais, daí escrevemos que:
Tranquilo?
Vem com a gente que vai ficar bem clarinho 😉
Passo 2
Gente, o sólido da nossa questão é algo parecido com isso daqui:
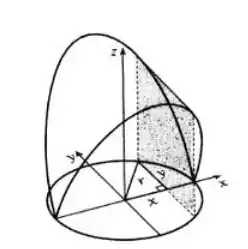
Bem esquisitinho né?
Bom, pensando em aplicarmos a nossa fórmula do método das seções transversais:
Temos que varia de até .
Além disso, o lado do quadrado da seção transversal, que depende de (metade do lado do quadrado), é dado por:
Porém, precisamos deixar essa expressão em função de . Daí, podemos usar o triângulo pitagórico destacado no sólido:
Logo:
Substituindo na integral, ficamos com:
Muito bom 😊
Passo 3
Agora vamos resolver a integral.
Portanto:
E aí, conseguiram entender direitinho?
Até a próxima gente!!