UFBA, Sem Campus, Cálculo B, Listas de Cálculo B - UFBA - Lista 1, Questão 2.1b
Determine o volume do sólido tal que:
A base de é a região parabólica , e as seções transversais perpendiculares ao eixo são triângulos equiláteros, com um lado na base.
Passo 1
Fala aí pessoal, tudo beleza?
Nessa questão temos um sólido cuja base é dada por:
E as secções transversais são triângulos equiláteros, com um dos lados nessa base.
Queremos calcular o volume desse sólido, beleza?!
Para fazer isso, vamos usar o método das seções transversais. Como as secções transversais foram tomadas perpendicularmente ao eixo , escrevemos que:
Onde varia de a .
Tranquilo?
Daí, precisamos conseguir escrever a área de uma secção transversal genérica em função de para depois substituir na integral e calcular o volume.
Vem com a gente que vai ficar bem clarinho 😉
Passo 2
A base do sólido pode ser esboçada da seguinte forma:
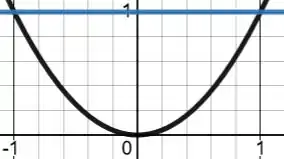
A seção transversal do sólido vai aumentando conforme aumenta o lado do triângulo equilátero nessa base. A relação entre o comprimento do lado do triângulo equilátero e a nossa variável , vem justamente da equação da parábola:
Onde é metade do lado do triângulo da secção transversal.
A área do triângulo equilátero, em função do lado do triângulo, é dada por:
Logo:
Daí, substituindo na integral, ficamos com:
Resolvendo essa integral, temos:
Prontinhoo!! Terminamos, gente!
Obrigado pela atenção de vocês 😊