UFBA, Sem Campus, Cálculo B, Listas de Cálculo B - UFBA - Lista 1, Questão 2.1e
Determine o volume do sólido tal que:
é uma calota de uma esfera de raio e altura .
Passo 1
Oii gente, tudo bom com vocês?
Nessa questão temos um sólido que é uma calota esférica, de raio e altura .
Precisamos determinar o volume dessa calota.
Para fazer isso, vamos usar o método das seções transversais. Vamos escolher um eixo para tomarmos as secções transversais da calota, chamando de eixo , vale que:
Tranquilo?
Daí, precisamos conseguir escrever a área de uma secção transversal genérica em função de para depois substituir na integral e calcular o volume.
Vamo nessa!
Passo 2
Vamos tomar como eixo a direção perpendicular à base da calota esférica.
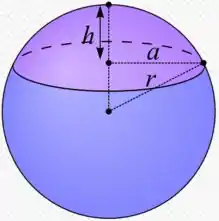
Nessa direção, a área da base é dada por:
representado na imagem é a altura total da calota, mas como vamos pegar infinitas secções, vamos chamar cada altura de . Onde:
onde é dado pelo triângulo pitagórico de catetos e hipotenusa . Daí:
Assim, temos:
Daí, substituindo na integral, temos:
Daí:
Portanto:
Prontinho!! Curtiram a solução?
Responde Aí!