UFCG. Cálculo Diferencial e Integral II. Listas de Cálculo 2 UAMat. Lista 3. Questão 3b.
3 - Determine o volume dos sólidos obtidos com a rotação, em torno do eixo , da região limitada pelas curvas:
(b) , .
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nessa questão temos que obter o volume do solido formado pela revolução em torno do eixo da área limitada pelas curvas e .
Primeiro de tudo vamos ver como é a área que vamos revolucionar e imaginar como será o objeto que vai se formar.
Esboçando as curvas no plano e hachurando nossa área de interesse, temos
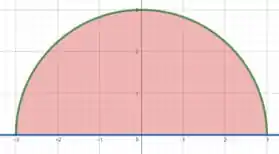
Como será nosso objeto ao revolucionar a área em vermelho em torno do eixo ?
Nossa área é um semicírculo e se revolucionarmos em , vamos obter uma esfera! Consegue ver isso?
Passo 2
Portanto, nosso objeto é formado como
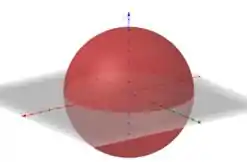
Podemos simplesmente aplicar a fórmula do volume da esfera, mas isso não teria graça nenhuma.
Então vamos usar o método dos discos. Esse método consiste em dividir o nosso sólido em infinitos discos perpendiculares ao eixo de raio e altura .
A fórmula do volume de um disco é dada por
No caso, cada volume infinitesimal tem raio que é a distância do eixo até a curva e em um valor infinitesimal
Fazendo essas substituições em , temos
Integrando nos dois lados, vamos obter
Legal, não é? 😁
Passo 3
Como é uma constante, podemos tirá-la da integral
Estamos interessados apenas no intervalo de entre e , então aplicamos esses valores como limites de integração
Obtemos a integral de uma constante como a própria constante multiplicada pela variável de integração, ou seja
Aplicando os limites de integração
Agora para a integral de aplicamos o método de integração polinomial, somando no expoente de e o dividindo pelo resultado da soma.
Aplicando os limites de integração...
Substituindo esses resultados em
Portanto, o volume do nosso solido é dado por !
É isso! Essa resolução te ajudou? Responde Aí! ✌
