Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 139123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFCG. Cálculo Diferencial e Integral II. Listas de Cálculo 2 UAMat. Lista 3. Questão 3e.

3 - Determine o volume dos sólidos obtidos com a rotação, em torno do eixo x , da região limitada pelas curvas:

(e) y = e - x , y = 0 , x = 0 , x = 1 .

Passo 1

Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nessa questão, temos que calcular o volume do sólido gerado pela rotação em torno do eixo x da área limitada pelas curvas y = e - x , y = 0 , x = 0 e x = 1 .

Mas como será que é essa região?

Plotando as curvas no plano x y e hachurando a região entre elas, temos

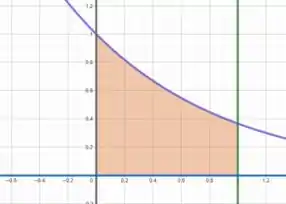
Imaginando essa área revolucionada ao redor do eixo x , vamos obter um solido parecido com uma rampa circular com o cume reto. Consegue ver isso? 🤔

Para obter o volume desse sólido, podemos aplicar o método dos discos! O que você acha? 😎

Passo 2

Esse método consiste em “fatiar” o sólido perpendicularmente ao eixo x com alturas infinitesimais.

O volume de um disco é dado por

V = π r 2 h

Perceba que em cada volume d V , o raio do risco é dado pela distância entre y = 0 e y = e - x , ou seja, r = e - x , já a altura h é dado por um valor infinitesimal em x que chamamos de d x .

Assim, o volume de cada disco é dado por

d V = π e - x 2 d x

Integrando dos dois lados, temos

∫ d V = ∫ π e - x 2 d x

V = ∫ π e - x 2 d x

Como a b c = a b c , então

V = ∫ π e - 2 x d x

Como π é uma constante, podemos tirá-la da integral...

V = π ∫ e - 2 x d x

Por fim, antes de começar a calcular o volume, estamos interessados apenas na região entre x = 0 e x = 1 , portanto, aplicando esses valores nos limites de integração, temos

V = π ∫ 0 1 e - 2 x d x

E finalmente podemos começar os cálculos! bora? 😁

Passo 3

Vamos calcular a integral de e - 2 x , pra isso, vamos fazer uma mudança de variáveis para facilitar nossos cálculos.

∫ e - 2 x d x

Substituindo - 2 x por u e derivando u com relação a x , temos

d u d x = d - 2 x d x = - 2

Isolando d x em um lado da igualdade...

d x = - 1 2 d u

Então substituindo - 2 x por u e d x por - 1 2 d u na integral...

∫ e - 2 x d x → ∫ e u - 1 2 d u

Tirando - 1 2 da integral

- 1 2 ∫ e u d u

Precisamos fazer essas mudanças também nos limites de integração. Antes x = 0 era o limite inferior e x = 1 o limite superior, agora como u = - 2 x , temos

u i = - 2 x = - 2 0

u i = 0

u s = - 2 x = - 2 1

u s = - 2

Aplicando esses limites...

- 1 2 ∫ 0 - 2 e u d u

Entendeu essa parte? 😉

Passo 4

Não podemos obter a integral de e u pelos métodos convencionais, então vamos apelar para o teorema fundamental do cálculo.

Pelo teorema, a integral de e u é igual a e u ...

∫ e u d u = e u

Aplicando os limites de integração, temos

∫ 0 - 2 e u d u = e - 2 - e 0 = e - 2 - 1

Substituindo esse resultado em V , lembrando que ∫ 0 1 e - 2 x d x = - 1 2 ∫ 0 - 2 e u d u , temos

V = π ∫ 0 1 e - 2 x d x

V = π - 1 2 e - 2 - 1

V = π 2 1 - e - 2

Portanto, o volume do solido que se forma é dado por π 2 1 - e - 2 ! Interessante, não é? 🤩

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta

V = π 2 1 - e - 2

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .