Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 731234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727475767778798081828384858687888990919293949596979899100

Enunciado

UFABC; Funções de Uma Variável; Listas FUV - GRADMAT; Lista 10 - Técnicas de Integração II ; Questão 8

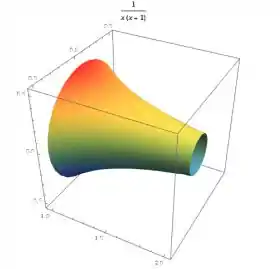
A região sob o gráfico de   y   = 1 x ( x   +   1 ) no intervalo [ 1 ,   2 ] é girado em torno do eixo   x . Encontre o volume do sólido gerado.

Passo 1

Fala galera, tudo bem com vocês? Vamos para mais uma questão de Cálculo 1. Essa questão tem como objetivo calcularmos o volume de um sólido de revolução gerado ao rotacionar a curva   y   = 1 x ( x   +   1 ) no intervalo [ 1 ,   2 ] é girado em torno do eixo   x

Vamos nessa!!!

Passo 2

A fórmula para calcular o volume de um sólido de revolução é bem conhecida, vocês lembram qual é?

Vamos dar uma revisada!!!

Seja f ( x ) uma função, então o volume do sólido gerado ao rotacionar f ( x ) em relação ao eixo x no intervalo [ a , b ] é:

V   = π ∫ a b ( f ( x ) ) 2 d x

Passo 3

Agora que relembramos a fórmula, vamos aplicar!!!

Nessa questão a f ( x ) é :

  y   = 1 x ( x   +   1 )

Então:

V   = π ∫ a b ( f ( x ) ) 2 d x

= π ∫ a b ( 1 x ( x   +   1 ) ) 2 d x

= π ∫ a b 1 x 2 ( x   +   1 ) 2 d x

Vamos usar frações parciais para simplificar essa integral. Para isso iremos encontrar A   ,   B ,   C   e   D tais que

1 x 2 ( x   +   1 ) 2   =   A x 2   + B ( x + 1 ) 2   + C x + D ( x + 1 )    

Passo 4

Vamos encontrar A   e   B tais que

1 x 2 ( x   +   1 ) 2   =   A x 2   + B ( x + 1 ) 2   - C x + D ( x + 1 )    

primeiro, desenvolvemos a igualdade

1 x 2 ( x   +   1 ) 2   =   A ( x + 1 ) 2 x 2 ( x + 1 ) 2   + x 2 B x 2 ( x + 1 ) 2 - C x ( x + 1 ) 2 x 2 ( x + 1 ) 2 + D x 2 ( x + 1 ) x 2 ( x + 1 ) 2  

então chegamos a conclusão que:

1   =   A x 2   +   2 A x   +   A   +   B x 2   -   C x 3   -   C 2 x 2   -   C x   +   D x 3   +   D x 2

⇒ 1   =   ( - C + D ) x 3 + ( A + B - 2 C + D ) x 2   +   ( 2 A - C ) x   +   A

Bem, aqui temos uma igualdade de polinômios em x isso quer dizer que os termos que têm x de um lado precisam ser iguais aos que tem x do outro lado da igualdade. Com isso temos:

A   =   1

2 A - C =   0

A + B - 2 C + D = 0

- C + D   =   0

Vamos resolver esse sistema!!!

Da última equação temos:

C = D

Da segunda equação temos:

2 - C   =   0

⇒ C = 2

⇒ D = 2

Usando esse resultado na terceira equação temos:

⇒ 1 + B - 4 + 2 = 0

⇒ B = 1

Passo 5

Usando os valores de A   ,   B ,   C   e   D que calculamos no passo anterior, chegamos a conclusão que

1 x 2 ( x   +   1 ) 2   =   1 x 2   + 1 ( x + 1 ) 2   - 2 x + 2 ( x + 1 )    

Então nosso volume fica:

π ∫ a b 1 x 2 ( x   +   1 ) 2 d x   = π ∫ a b 1 x 2   + 1 ( x + 1 ) 2   - 2 x + 2 ( x + 1 ) d x  

Pela linearidade da integral

= π ( ∫ a b 1 x 2 d x   + ∫ a b 1 ( x + 1 ) 2 d x   - ∫ a b 2 x d x + ∫ a b 2 ( x + 1 ) d x )

mas essas integrais são bem conhecidas. Então

= π ( - x - 1   - ( x + 1 ) - 1   - 2 l n ( | x | ) + 2 l n ( | x + 1 | ) ) | x = b x = a

Agora calculamos no intervalo [ 1,2 ]

= π ( - 2 - 1   - ( 2 + 1 ) - 1   - 2 l n ( | 2 | ) + 2 l n ( | 2 + 1 | ) )   -   π ( - 1 - 1   - ( 1 + 1 ) - 1   - 2 l n ( | 1 | ) + 2 l n ( | 1 + 1 | )

juntando tudo

π ( - 1 2 - 1 3   -   2 l n ( 2 )   +   2 l n ( 3 )   + 1 + 1 2   - 2 l n ( 2 ) )

= π ( 2 3   - l n ( 16 9 ) )

Prontinho pessoal. Com isso terminamos mais uma questão de Cálculo 1. Tivemos umas “simplificações” bem diferentes na resolução dessa questão, além de revisarmos a fórmula do volume de um sólido de revolução. Espero que os passos tenham ficado claros. Até a próxima!!!

Resposta

= π ( 2 3   - l n ( 16 9 ) )

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .