Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 126123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Cálculo de Volumes através de Integrais

Seja R = x , y   ϵ   R 2 : 1 ≤ x ≤ e ,   1 ≤ y ≤ 2 + ln ⁡ x . Calcule o volume do sólido obtido pela rotação de R em torno da reta y = 3 .

Passo 1

Vamos desenhar a região, esclarecendo aonde ficam os gráficos, o eixo e os limites de integração, dado que f 1 = 2 + ln ⁡ ( 1 ) = 2 e f e = 2 + ln ⁡ ( e ) , onde eu chamo de f ( x ) o limite superior para o y .

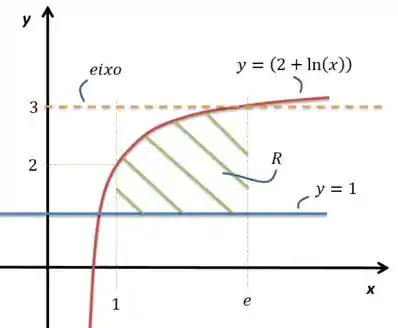
Certo, substituindo os limites de x em diagrama com os de y a gente vai achar essa região aí. Repara que o eixo é esse em laranja aí. Tá, já é muito claro, ainda mais com a figura, que os limites de integração vão acabar sendo os do x , de 1 até e . Dado isso, Basta descobrirmos qual é a integral pelo método das seções transversais. A gente tem como fórmula que o volume de uma função f ( x ) girando num eixo y = L será:

V = ∫ a b π f x - L 2 d x

Bom, pelo desenho nós teremos que fazer uma diferença entre o giro de duas funções: a de y = 1 por fora, já que está mais afastada do eixo, menos a de y = 2 + ln ⁡ x , que está mais próxima a esse mesmo eixo.

Assim, essa diferença de volumes pode ser calculada desse jeito:

∫ 1 e π 1 - L 2 d x - ∫ 1 e π 2 + ln ⁡ ( x ) - L 2 d x

Agora é mão na massa e acabou, irmão. Botando L = 3 e unindo as equações vai sair assim:

∫ 1 e π 1 - 3 2 - π 2 + ln ⁡ x - 3 2 d x = ∫ 1 e π - 2 2 - π ln ⁡ x - 1 2 d x

= π ∫ 1 e 4 - ln 2 ⁡ x + 2 ln ⁡ x - 1 d x

= π ∫ 1 e 3 - ln 2 ⁡ x + 2 ln ⁡ x d x

Bom, vou integrar cada um dos termos para depois juntar tudo. A integral de 3 é 3 x , nenhum problema até aí. A de ln ⁡ ( x ) é por definição assim:

∫ ln ⁡ ( x ) d x = x ( ln ⁡ ( x ) - 1 )

Caso complique para visualizar, é só você resolver essa de cima por partes e vai ver que o resultado é esse. Agora, a outra vai dar um trabalhinho a mais, só que sai por partes também. Usamos o LIATE para definir o u e o d v .

∫ ln 2 ⁡ ( x ) d x     ,           u = ln 2 ⁡ ( x ) ; d v = d x

d u = 2 ln ⁡ x x ; v = x

∫ ln 2 ⁡ ( x ) d x = x ln 2 ⁡ ( x ) - ∫ 2 ln ⁡ ( x ) d x

= x ln 2 ⁡ ( x ) - 2 x ln ⁡ x - 1

Ok, voltamos para integral original:

= π ∫ 1 e 3 - ln 2 ⁡ x + 2 ln ⁡ x d x

π 3 x - x ln 2 ⁡ x + 2 x ln ⁡ x - 1 + 2 x ln ⁡ x - 1 [ e 1

= π 3 x - x ln 2 ⁡ x + 4 x ln ⁡ x - x [ e 1 = π - x - x ln 2 ⁡ x + 4 x ln ⁡ x [ e 1

= π - x ( 1 + ln 2 ⁡ x - 4 ln ⁡ x [ e 1

= π - ( e ) ( 1 + ln 2 ⁡ e - 4 ln ⁡ e - π - 1 ( 1 + ln 2 ⁡ 1 - 4 ln ⁡ 1

= π - e - 2 - π - 1 1

= π ( 2 e + 1 )

Resposta

V = π 2 e + 1   u . v .

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .