Seja a região delimitada pelas curvas .
- Esboce a região .
- Escreva as integrais que determinam o volume do sólido obtido pela rotação da região acima ao redor da reta pelo método das cascas cilíndricas e pelo método dos discos.
- Calcule o volume pedido.
Passo 1
Vamos começar esboçando a região. é espelhado, ficando:
Apesar de parecer o contrário no gráfico, nunca toca o eixo , confie em mim!
Agora é só colocar as retas e . A região é aquela bordeada por essas curvas:
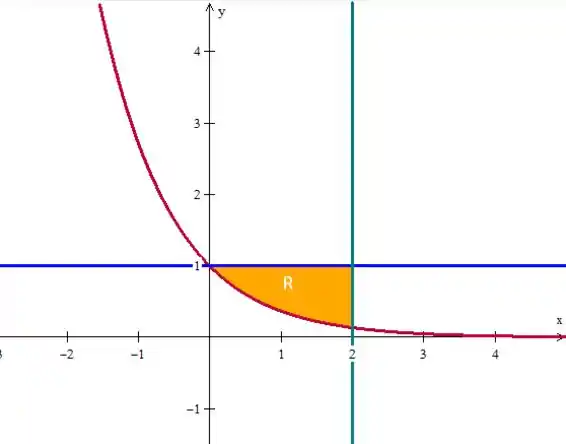
Passo 2
Vamos agora observar a região para construir as integrais do volume. Veja que a região começa na interseção entre a reta e , em , sendo esse o limite de integração inferior. E termina na reta , sendo o limite superior de integração.
Começando pelo método dos discos cilíndricos, temos:
Como desejamos girar em torno da reta , teremos e a curva mais perto será . Da mesma forma, :
O método das cascas cilíndricas é geralmente usado para rotação em torno de uma reta vertical. Nesse caso, porém, temos uma reta horizontal . Para usá-lo, precisamos integrar em relação a :
Para o limite de integração inferior, quando , temos que , então . Para o superior, quando , , então .
será a a constante da reta que estamos girando, ou seja e será a curva do caso anterior, mas em função de :
será a própria reta . Assim sendo, escrevemos:
Passo 3
Vamos agora resolver a integral para calcular o volume. Vamos fazer pelos discos cilíndricos que é mais fácil:
Para calcular a integral, vamos distribuir o integrando:
Ficando:
Logo:
Não esquecendo o u.v. que indica unidade de volume.
Se você calculasse pelas cascas cilíndricas, o resultado seria o mesmo.
Resposta
Ei, a resposta está no passo a passo :)