Seja a região limitada pelas curvas e .
(a) Esboce e calcule a sua área.
(b) Calcule o volume do sólido gerado pela rotação de em torno do eixo .
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

O enunciado da questão nos disse que temos uma região limitada por duas curvas dadas por e .
Com base nessas curvas temos que desenhar e calcular a área entre essas curvas e depois disso ainda temos que calcular o volume de um solido que é gerado pela rotação de em torno do eixo .
E aí! Tem ideia de como fazemos isso? 🤔
Para o item a) vamos desenhar os as curvas no plano , obter a região e calcular sua área.
E no item b) vamos aplicar um método de revolução que chamamos de método dos discos e calcular o volume gerado por essa revolução.
Ta curioso? Bora ver como vai ficar! 😁
Passo 2
Primeiro vamos desenhar a região . Plotando as curvas , que é uma reta que divide os quadrantes ímpares no meio, e que é uma curva muito parecida com o paraboloide , temos
A reta verde representa a equação e a curva vermelha a equação .
Hachurando a região entre as curvar, vamos obter a região !
Veja só!

Logo essa região azul é a região que procuramos.
E para calcular a área da nossa região vamos calcular a sua integral.
Lembra que a integral nos dá a área abaixo de uma curva? Então podemos ler a área da região como a área abaixo da reta azul, menos a área abaixo da curva vermelha, correto?
E os limites de integração são os valores do intervalo de que contem a região .
Pelo gráfico, vemos que esse intervalo acontece entre as intersecções de e , ou seja
Para essa equação ser satisfeita, deve ser ou deve ser .
Logo nosso intervalo de integração é
Tranquilo até aqui? 😎
Passo 3
Com essas informações podemos escrever nossa integral como
Integrando pelo método de integração polinomial, onde somamos no expoente da variável e a dividimos pelo resultado da soma no seu expoente
Aplicando os limites de integração, temos
Com isso, encontramos a área da nossa região ! Entendeu?
Agora para calcular o volume gerado pela revolução da nossa região, vamos aplicar o método dos discos.
Rotacionando uma curva em torno de um eixo, vamos obter um disco em cada sessão perpendicular a nosso eixo de rotação. Concorda?
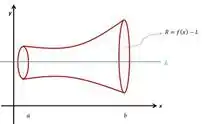
Dessa forma cada disco de comprimento infinitesimal terá um pequeno volume, integrando a área do disco onde o raio do disco é dado pela distância da curva até o eixo de rotação, vamos obter o volume do disco.
Ou seja, aplicamos a equação que descreve a área de um disco substituindo pela curva de revolução.
Interessante, não é?
Passo 4
Aqui segue a mesma ideia da área da região, o volume que procuramos é o volume da revolução abaixo de menos a revolução abaixo de .
Como a área de um círculo é , nossa função de integração será
Onde é a distância de e é a distância de , ou seja
Com isso, nossa integral será
Organizando um pouco mais a nossa integral, vamos ter
Integrando pelo mesmo método de integração polinomial, temos
Aplicando os limites de integração
Com isso, vemos que o volume da nossa região revolucionada em torno do eixo é de !
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
a)
b)