Seja a região limitada do plano, que é delimitada pelos gráficos das curvas e , consideradas para valores .
a) Esboce a região , indicando os pontos de interseção das curvas
b) Calcule o volume do sólido obtido ao girar a região em torno da reta
Passo 1
Show! Pra começar, vou te dizer que nem precisa grilar muito com o esboço. A gente só precisa esboçar o suficiente pra poder entender a região que estamos rotacionando. Com ovamos precisar das interseções das curvas, um bom primeiro passo é fazer:
Logo:
Como o enunciado diz que ta valendo pra , temos os dois pontos me que a nossa região se fecha:
E saca só, qualquer número ao cubo entre e fica menor que ele mesmo. Veja por exemplo:
Sendo assim, nesse intervalo todo a curva vai estar sempre por baixo! Temos o suficiente pra esboçar! Vamos ter:
Passo 2
Passo 3
Show, agora pra rotacionar essa região em torno de , vamos lembrar do método dos discos:
Os limites de integração vão ser aqueles que fecham a região mesmo, a malandragem está em definir quem é . Como representa o raioda rotação ao longo da horizontal , perceba, por exemplo, que pra reta , o raio, em vermelho, tem sempre o seguinte tamanho:
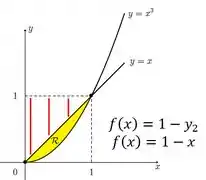
E pra reta , o raio, em vermelho, tem sempre o seguinte tamanho:
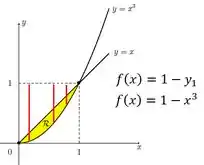
Como o raio da curva é maior, o volume da rotação dela também vai ser! Então o volume da região vai ter que ser uma subtração de um volume maior por um volume menor! De forma que:
Substituindo os valores que a gente achou, temos:
Passo 4
Agora é mão na massa mesmo! Vamos calcular esse limite. Pra começar, vamos abrir os quadrados:
Juntando tudo em uma única integral:
E agora, resolvendo a integral, temos:
Colocando no mesmo denominador
Olha, todos os termos tem mesmo, e como um dos limites de integração é zero, nem precisamos esquentar a cabeça. A resposta no final das contas vai ser exatamente o que está escrito em cima, trocando todos os termos de por . Logo: