1) Seja a região plana dada pelo esboço abaixo:
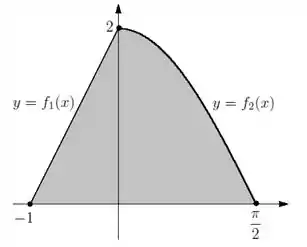
Onde e são funções tais que:
- O gráfico de é uma reta que passa pelos pontos e .
- , onde são constantes reais
Responda:
- Determine a expressão de e
- Seja o sólido de revolução obtido pela rotação da região em torno do eixo . Utilizando o método que preferir, escreva o volume de como uma integral ou uma soma de integrais.
- Calcule o volume de pelo método que preferir.
Passo 1
Bora lá começar então! O gráfico nos dá todas as dicas pra achar a expressão de e . Pra começar, a função , que é uma reta, tem a seguinte expressão:
Já que sabemos dois pontos em que essa função passa, basta substituirmos esses valores. Partiu:
E logo:
Agora pra temos:
A ideia vai ser a mesma, só precisamos substituir pelos pontos que sabemos que a curva passa. Nesse caso:
Vamos ter:
Concluímos então que:
Passo 2
Beleza. A questão agora quer que a gente revolucione a região em torno do eixo e ache o volume. Tem um método esperto que faz exatamente isso. Pelo método dos anéis, temos:
Show, vamos adequar então essa integral a nossa realidade. Quando rotacionamos somente , ficamos com:
Isso porque a reta não ta definida pra valores menores que e nem maiores que . Do em diante temos o cosseno! Mas olha só, ele também para num ponto: o ponto . Então estão ai os limites de integração do cosseno rotacionado:
E como a região hachurada é exatamente o espaço abaixo de e até o eixo , o volume da região interia rotacionada vai ser nada mais nada menos do que a soma desses dois aí em!:
Passo 3
Agora é só calcular o volume. Abrindo os quadrados, temos:
Como:
Ficamos com:
Aplicando a substituição simples na última integral::
Ficamos com:
E agora a resolução é direta! Vamos ter:
Para o primeiro termo dentro do colchete:
Para o segundo termo:
E pro terceiro:
Juntando tudo: