Sejam e funções dadas por
𝑒 considere a região plana descrita abaixo:
Seja o sólido gerado pela rotação da região em torno do eixo
a) Esboce a região plana
b) Escreva o volume de utilizando o Método de Discos ou método de cascas ciníndricas.
Obs: Neste item não é necessário calcular o volume.
Passo 1
a) Para o esboço temos
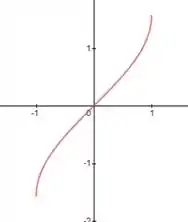
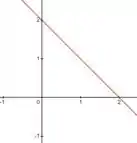
Juntando temos
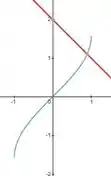
No entanto, nosso x vai só de zero até o que nos dá essa região.
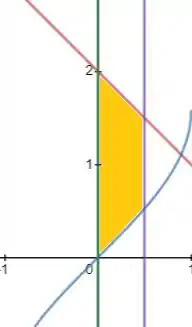
Passo 2
b) Aplicando o método dos discos:
Lembrese que estamos rodando em volta do eixo x, logo, nossa integral vai ser em relação a x, ok? (dx) Como nosso x varia entre 0 e , teremos para os raios internos e externos
Então o volume é dado por
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .