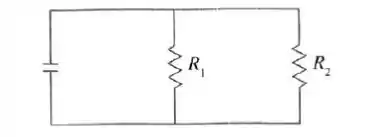
Se dois resistores com resistências e estão conectados em paralelo, como na figura, então a resistência total , medida em ohms (, é dada por
Se e estão crescendo a taxas de e , respectivamente, quão rápido estará variando quando e ?
Passo 1
Primeiramente, derivando a função em relação ao tempo em segundos temos:
Passo 2
Quando e , então é dado por:
Passo 3
Portanto, quando , ,, e , temos:
Logo, a taxa com que varia é .
Resposta
A taxa com que varia é .