UTFPR - Sem Campus - Cálculo Diferencial e Integral 1 - Provas - Teste 9 - AV2 - 2022.1 - Questão 5 - Alternativa a)
Suponha que é dada implicitamente pela equação . Suponha que .
Calcule .
Passo 1
Eaew, tudo certinho?
O enunciado nos deu uma definição implícita de uma função , da seguinte forma
a definição ser implícita tem relação com o fato que não está escrita exatamente no formato de . O enunciado pede para que suponhamos e que calculemos . Para fazer isso precisamos substituir o valor de desejado e tentar isolar a função . Vamos lá!
Passo 2
Temos que quando usamos na função dada, obtemos
Jogando o para o lado esquerdo com sinal negativo (ou subtraindo quatro dos dois lados) temos que
Em geral temos que um polinômio de terceiro grau tem raízes. Se soubermos uma raiz podemos utilizar o método de Briot Ruffini para verificar a existência de outras raízes reais. Para podermos descobrir quem é a raiz inicial vamos primeiro identificar os divisores do termo independente do polinômio. Como o nosso termo independente é , temos que os divisores serão
Ou seja, quatro possibilidades de chute! O chute já é uma raiz, portanto, não precisamos verificar os outros chutes! Vamos relembrar o método para a redução de ordem! Saca só!
Passo 3
O método para reduzir a ordem do polinômio pode ser resumido com esse procedimento que coloquei na tabelinha abaixo
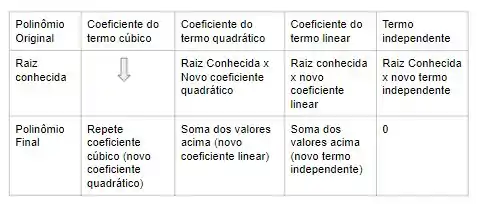
A raiz conhecida é que achamos no passo anterior, o coeficiente do termo cúbico é , o coeficiente do termo quadrático é , o coeficiente linear é e o termo independente é , então podemos aplicar o procedimento acima para obter
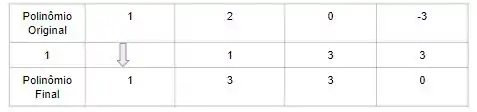
Portanto, nosso novo polinômio pode ser identificado como
Se aplicarmos Bhaskara para obter as outras raízes, temos que
Ou seja, são raízes imaginárias. Portanto, a única solução real para nosso problema é
Essa foi a primeira alternativa! Bora para a próxima! Até daqui a pouco!