7. Uma escada de está encostada em uma parede. Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de , com que velocidade a extremidade superior estará descendo no instante em que a inferior estiver a da parede?
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos um probleminha de taxa relacionada e para entender o que está acontecendo, vamos montar uma figura:
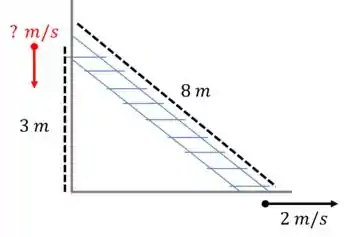
Repara que desenhando o que problema descreve temos uma triangulo retângulo. Onde a nossa hipotenusa é o tamanho da escada e tem e os catetos são a altura da parede e a distancia do pé da escada até a parede.
O problema disse que o pé se afasta a uma taxa de . Ou seja, conforme aumentamos a distância do pé da escada até a parede, diminuímos a altura de apoio da escada na parede.
E o problema nos pergunta exatamente isso, qual a velocidade em que essa altura diminui no ponto onde a altura é igual a . Ou seja, temos que relacionar a taxa de variação da distância horizontal com a taxa de diminuição da altura.
Bora lá!
Passo 2
A gente começa estabelecendo uma relação entre os lados do triângulo. Como temos um triângulo retângulo, vamos usar o Teorema de Pitagoras.
Passando isso para o nosso problema, temos
Vamos simplificar e adotar letras para cada variável,
Onde é altura e é a distância horizontal.
Mas aqui queremos relacionar a taxa de variação de com a de . Então vamos derivar essa função!
Passo 3
Mas repara que temos uma função implícita (ou seja, e não estão isolados) para derivar. E quando derivamos implicitamente.
Derivando,
Como queremos a variação da altura, vamos isolar
Agora vamos substituir com os dados fornecidos pelo enunciado!
Passo 4
A extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de . Ou seja,
O problema nos pede a velocidade a extremidade superior estará descendo no instante em que a inferior estiver a da parede. Ou seja,
E para acharmos , podemos aplicar o Teorema de Pitagoras,
Logo,