O fólio de Descartes
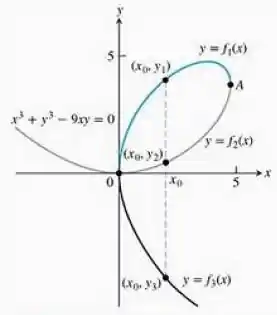
Encontre o coeficiente angular do fólio de Descartes, nos pontos e
Em qual ponto, além da origem, o fólio tem uma tangente horizontal?
Encontre as coordenadas do ponto da figura, onde o fólio tem uma tangente vertical.
Passo 1
O cara nos pediu o coeficiente angular,. O que eu te contei na teoria? O coeficiente angular é a derivada da função avaliada nos pontos que ele nos deu. Então vamos precisar derivar a expressão do fólio.
Passo 2
Vamos achar a derivada por Derivação Implícita:
Observa que para o termo , vamos precisar usar a regra do produto
Passo 3
Aplicando os pontos, ficamos com:
Passo 4
Ele pede que achemos o ponto onde a tangente é horizontal.
Ora, uma reta horizontal tem inclinação zero, ou seja, seu coeficiente angular é nulo. Portanto, o que queremos achar é:
Ou seja, todos os pontos que satisfazem essa igualdade vão zerar a derivada.
Passo 5
Para encontrar o ponto que vem dessa igualdade, jogamos ela na equação da curva:
Multiplicando tudo por
Como ele pede para desconsiderar o ponto da origem, a solução não nos interessa.
Passo 6
O para esse valor de vai ser:
O ponto será, portanto:
Passo 7
Ele pede que achemos uma tangente vertical agora.
Ora, uma reta vertical tem inclinação “infinita”, ou seja, seu coeficiente angular é explode para . Portanto, o que queremos achar é:
Isso acontecerá quando o denominador zerar sem que haja indeterminação . Ou seja, queremos que
Para encontrar o ponto que vem dessa igualdade, jogamos ela no termo inicial:
Passo 8
Como ele pede para desconsiderar o ponto da origem, a solução não nos interessa.
O para esse valor de vai ser:
O ponto será, portanto: