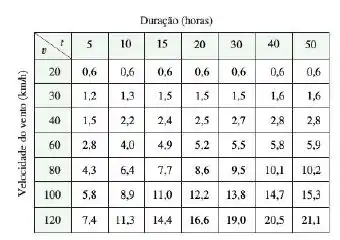
A altura de ondas em mar aberto depende da velocidade do vento e do tempo durante o qual o vento se manteve naquela intensidade. Os valores da função são apresentados na tabela abaixo:

1. Qual o significado das derivadas parciais e ?
2. Estime os valores de e . Quais são as interpretações práticas desses valores?
3. Qual parece ser o valor do limite ?

Queremos as derivadas parciais de no ponto , certo?!

Vamos começar pela taxa de variação em relação a .

Para isso, fixamos o valor de como uma constante, igual 15. Assim, ficamos com uma função que depende só de :

Então, só precisamos calcular a derivada no ponto e teremos a taxa de variação de em relação a . Assim, pela definição de derivada de uma variável, para :

Beleza, então agora é só substituir tudo e calcular esse limite. Mas, pera! A gente não tem a expressão de , como vamos substituir então?

Bem, nesse caso, temos que fazer o variar, por exemplo, fazendo , para que possamos pegar os valores de na tabela.

Depois, fazemos a média dos valores calculados quando fizemos e para determinar a .

Parece confuso né? Mas olha só como é:

Fazendo primeiro :

Agora :

Para achar temos que fazer a média desses dois valores. Assim:

Isso nos diz que quando a duração do vento é de 15 horas, a altura h aumenta de a cada .

Agora, para a taxa de variação em relação a fazemos a mesma coisa.

Considerando constante e igual a 80, temos uma função que depende só de :

E então, para achar , fazemos:

E, agora fazemos , para poder pegar os valores na tabela e temos:

Para :

Para

Por fim, fazemos a média desses dois valores e temos que

Isso nos diz que para a velocidade de , a altura h da onda aumenta de por cada 5 de duração do vento.

Olhando a tabela, vemos que, mantendo um fixo, a medida que cresce, parece que os valores de tem uma variação muuuito pequena, quase zero. Então, parece que