UTFPR– Cálculo 2 – Lista 2022.2 – Questão 3
As dimensões de uma caixa retangular fechada foram medidas como e , respectivamente, com erro máximo de em cada dimensão. Utilize diferenciais para estimar o máximo percentual de erro no cálculo da área da superfície da caixa
Passo 1
Oi, tudo bem? Esse problema parece complicado, mas vou te ajudar! Temos uma caixa fechada com dimensões , tipo assim
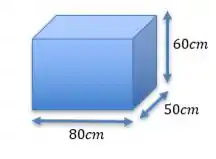
E em cada dimensão temos um erro máximo de . O problema pede para usar diferenciais e estimar o erro percentual no cálculo da área da superfície dessa caixa
É o que?
O erro percentual de alguma função é calculado assim
Onde é o diferencial, ou seja, a derivada da função. Queremos saber o erro no cálculo da área superficial, então nossa função é aquela que representa a área da superfície dessa caixa!
Digamos que nossa caixa tenha dimensões , então a função área vai ser
Lembrando que é uma caixa fechada, então contamos duas vezes todas as faces!
E o diferencial vai ser o erro máximo da área, dado por:
E os diferenciais são os erros máximos das dimensões , ou seja, em cada dimensão!
E em que ponto vamos aplicar essa derivada? No ponto em que as dimensões sejam os valores medidos, ou seja:
Tranquilo?
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Vamos dizer que a altura da caixa é , o comprimento é e a largura é , então a área da sua área é
Para estimar o erro usando diferencial, vamos achar as derivadas parciais
Então temos
Tudo bem até aqui?
Passo 3
Como o enunciado nos diz que o erro máximo de aferição é de , vamos usar , para estimar o máximo de erro, assim
Com e , agora é só substituir!
Esse é nosso erro no diferencial! Agora nossa missão é encontrar o erro percentual
Passo 4
O erro percentual é
Do passo : , mas precisamos saber a área quando as dimensões são e :
Agora o erro percentual é
E é isso galera! Vamos para a próxima?