Regra da Cadeia, Derivadas Parciais e o Vetor Gradiente
Seja , em que é uma função diferenciável de uma variável real. Verifique que
Passo 1
Queremos verificar essa relação, que envolve as derivadas parciais de , então vamos calculá-las! Vamos ter que usar a regra da cadeia e a regra do produto:
Repare que então, pra outra derivada parcial vamos ter:
O que dá:
Passo 2
Show de bola, agora vamos verificar a equação!
Poxa, ficou tão grande :( Mas não adianta chorar, agora é arregaçar as mangas e partir pras contas! Isso vai dar:
Opa! Vai dar pra cortar 2 desses troços estranhos!
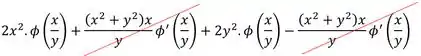
Então sobrou:
Beleza! Conseguimos provar a equação! :D
Resposta
Exercícios de Livros Relacionados
Encontrar a inclinação da reta tangente à curva resultante da intersecção de z = f ( x , y ) com o plano x = x 0 no ponto P ( x 0 , y 0 ,z 0 ) .a) z = x 2 + y 2 - 1 ; P ( 1 ,- 1 ,1 )
Mostre que a função produção de Cobb-Douglas satisfaz P L , K 0 = C 1 K 0 L α resolvendo a equação diferencial d P d L = α P L
No estudo de penetração do congelamento descobriu-se que a temperatura T no instante t (medido em dias) a uma profundidade x (medida em pés) pode ser modelada pela função T ( x , t ) = T 0 + T 1 e - λ
80. A temperatura em um ponto x ,y de uma chapa de metal é dada por T x ,y = 60 / ( 1 + x 2 + y 2 ) , onde T é medido em ° C e x , y em metros. Determine a taxa de variação da temperatura no ponto 1 ,
Seja ϕ : R → R uma função diferenciável tal que ϕ ' 3 = 4 . Seja g x , y , z = ϕ x 2 + y 2 + z 2 . Calcule:a) ∂ g ∂ x 1,1 , 1 b) ∂ g ∂ y 1,1 , 1 c) ∂ g ∂ z 1,1 , 1