![]()
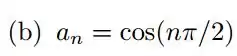
Passo 1
Primeiramente, vamos relembrar como calculamos o limite de uma sequência :
No nosso caso, ficamos com:
Se esse limite existe e for um número, a sequência converge e o limite dela é este número. Caso contrário, ela diverge.
Passo 2
Perceba que estamos lidando com uma função periódica. Você multiplicar ou dividir o ângulo ali dentro do cosseno não muda em nada o fato dele ser periódico, você só muda o período. Dá uma olhada no gráfico:
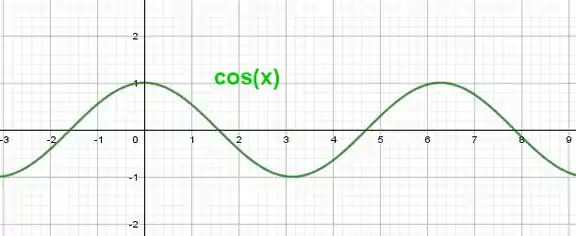
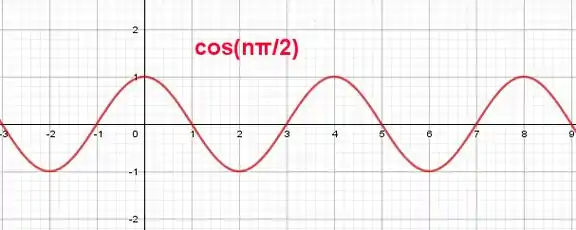
Note que estamos vendo a função, que aceita um que não seja inteiro. Porém, a função se comporta igualmente a sequência, pros casos de inteiro, então a gente pode tentar visualizar como se fossem a mesma coisa sem problemas!
Agora olhe os dois juntos:
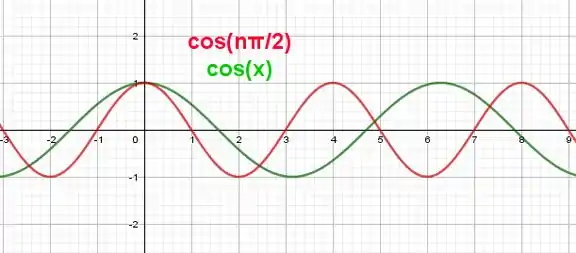
Viu só? Apenas mudou o período. Continua sendo periódica e, sendo assim, o limite não existe, pois fica variando entre e .
Resposta
O limite não existe.