Calcule o limite da sequência:
Se ela for convergente.
Passo 1
Vamos escrever a função associada a esta sequência: basta trocar por :
E agora vamos buscar o limite (se convergir). Para isso, temos que analisar .
Passo 2
Esse limite ta complicado de resolver de cara, então vamos reescrever essa função de outra forma para ver se facilita.
Repara que a gente aplicou uma propriedade de potência e chegamos um limite que pode ser resolvido através do limite fundamental exponencial. Lembrando que o limite fundamental é dado como:
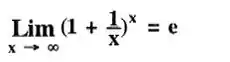
Nesse caso, teremos que:
Fazendo , temos que:
Então agora é só resolver o que está dentro dos colchetes:
Portanto:
Resposta
.