Calcule os limites laterais de em , se .
Passo 1
Primeiro, vamos escrever como fica a definição de :
Passo 2
Agora calculamos os seguintes limites laterais, que ele pediu.
Só fica ligado numa coisa: quando , ou seja, , usaremos a primeira expressão para . Quando , ou seja, , usaremos a segunda expressão para
No primeiro limite, vou substituí-lo:
Da mesma forma que o primeiro, vou começar substituindo esse segundo limite lateral também:
Passo 3
Vamos começar no primeiro limite. Nesse caso, vou trazer o círculo trigonométrico para pensarmos sobre o sinal desse “infinito”, se é positivo ou negativo:
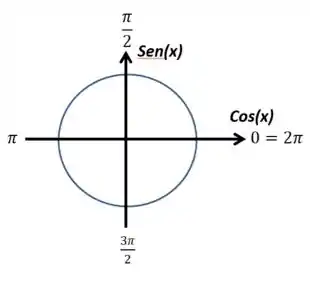
Repara que, para valores logo acima de (valores um pouquinho maiores que ), o seno é positivo. Com isso:
Portanto,
Passo 4
Olhando para o mesmo desenho de antes, vamos reparar que o seno é negativo para valores logo antes de (valores pouco menores que ). Logo,
Portanto,