Resolva o seguinte limite:
Passo 1
Vamos, antes de tudo, lembrar o que é . A secante é basicamente dada por:
Passo 2
Dessa forma, substituindo o na equação, ficaria assim:
A gente já tem noção que isso vai dar . Resta saber como estamos nos aproximando de .
Passo 3
Pensando nessa análise do sinal, você percebe que a aproximação é feita por trás, ou seja, para valores menores que . Vamos dar uma olhada no círculo trigonométrico para matar a charada.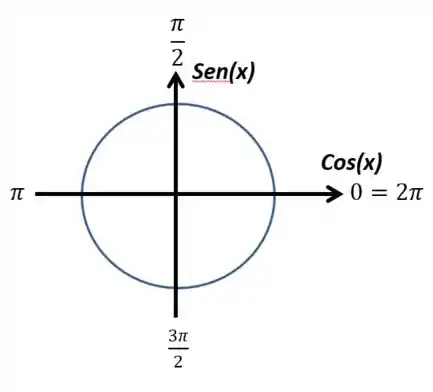 
Bom, podemos ver que, quando x está vindo por trás de (lembrando que ), temos cosseno negativo. Dessa forma, podemos dizer que a aproximação se dará para . Portanto,
Resposta
Exercícios de Livros Relacionados
Faça o gráfico da função f x = sin π x do Exemplo 4 na janela retangular - 1,1 por - 1,1 . Então dê um zoom em direção à origem diversas vezes. Comente o comportamento dessa função.
Estime o valor do limite lim x → 0 1 + x 1 x Com 5 casas decimais. Esse número lhe parece familiar?Confirme sua resposta da letra (a) fazendo o gráfico da função.
Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas.14)lim x → 0 - f x = 1 , lim x → 0 + f x = - 1 ,lim x → 2 - f x = 0 ,lim x → 2 + f x = 1 , f 2 = 1 ,f 0
Use o gráfico da função f x = 1 1 + e 1 x Para dizer o valor de cada limite, se existir. Se não existir, explique por quê. lim x → 0 - f x lim x → 0 + f x lim x → 0 f ( x )
Para a função f cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, diga o por quê. lim x → 1 - f x lim x → 1 + f x lim x → 1 f x lim x → 5 f x f ( 5