UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - UNICAMP - Lista 3 - Limite e Continuidade. Questão 39
Dê exemplo de uma função tal que existe, mas não exista.
Passo 1
Eaew, tudo certinho?
O enunciado é bastante direto, precisamos dar exemplo de uma função tal que
e, o limite
Então, vou dar um exemplo em que os limites laterais ao redor de um ponto são diferentes em um caso e iguais no outro! Saca só!
Passo 2
Se considerarmos a função
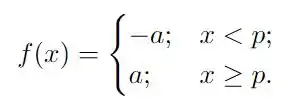
em que é uma constante e é um ponto, qualquer, note que se calcularmos os limites laterais
e
já que em um caso estamos considerando valores menores que e no outro valores maiores que . Note que como
então o limite não existe! No entanto, se calcularmos o módulo da função nas mesmas condições, temos que
e, sendo assim, agora temos
e, o limite existe! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!
Exercícios de Livros Relacionados
Faça o gráfico da função f x = sin π x do Exemplo 4 na janela retangular - 1,1 por - 1,1 . Então dê um zoom em direção à origem diversas vezes. Comente o comportamento dessa função.
Estime o valor do limite lim x → 0 1 + x 1 x Com 5 casas decimais. Esse número lhe parece familiar?Confirme sua resposta da letra (a) fazendo o gráfico da função.
Esboce o gráfico de um exemplo de uma função f que satisfaça a todas as condições dadas.14)lim x → 0 - f x = 1 , lim x → 0 + f x = - 1 ,lim x → 2 - f x = 0 ,lim x → 2 + f x = 1 , f 2 = 1 ,f 0
Use o gráfico da função f x = 1 1 + e 1 x Para dizer o valor de cada limite, se existir. Se não existir, explique por quê. lim x → 0 - f x lim x → 0 + f x lim x → 0 f ( x )
Para a função f cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, diga o por quê. lim x → 1 - f x lim x → 1 + f x lim x → 1 f x lim x → 5 f x f ( 5