Calcule os seguintes limites laterais:
Passo 1
Assim como qualquer resolução de limites, a boa é começar substituindo o na função do limite, para termos uma ideia do que acontece. Ficaria algo assim:
As aspas indicam que a operação não é formalmente válida. Estamos indicando que, quando o denominador se aproxima de zero, a fração tende para o infinito.
Agora, o detalhe é que estamos calculando limites laterais, então falta analisar o comportamento pelos lados do . Repara que ali eu coloquei por que ainda não sei se ao aproximar do eu venho por um número levemente maior ou levemente menor.
Isso faz com que resulte em algo um pouquinho maior ou um pouquinho menor que , respectivamente (ou seja, um é positivo e outro negativo).
Passo 2
Faz o seguinte, chuta um número abaixo e outro acima de . Olha o que acontece com e , por exemplo:
Sacou? Assim, o que acontece é que pelo lado do 5 (atrás do 6) a função se aproxima negativamente e pelo lado do (na frente do 6) se aproxima positivamente.
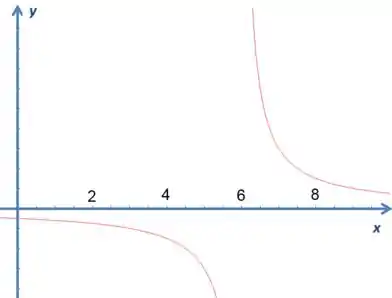
Ainda não acredita? Desenhei aqui o gráfico para os incrédulos: