Esboce o gráfico da função a seguir e use-o para determinar os valores de para os quais
existe:
Passo 1
Beleza, vamos analisar a função. São 3 intervalos de função. Vamos fazer o seguinte, primeiro desenhar esse negócio aí. Temos a função de primeiro grau quando então o gráfico antes de igual a vai ser essa reta.
Na parte onde está entre e ele vai ser a reta . E quando vamos ter a parte da parábola . O gráfico vai ficar então:
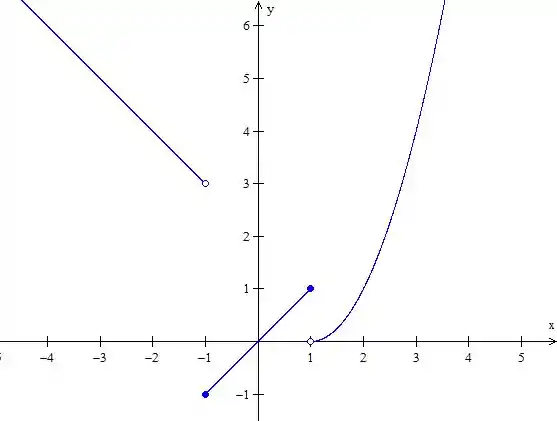
Passo 2
Passo 3
Então, já que a estrutura está montada, vamos olhar no gráfico os pontos onde
existe, ou seja, onde vale:
Passo 4
Cara, conseguimos ver que esses limites existirão para todosem que a função não muda sua lei de formação.
Resumindo, para que o limite lateral seja igual, os pontos teriam que seguir o mesmo padrão dos dois lados ou ter o limite entre os pontos onde trocam-se os regimes de função dando a mesma coisa.
A princípio, todos os pontos fora e terão limites laterais iguais. Resta saber se esses dois pontos têm limites laterais iguais.
Passo 5
Pelo desenho, vemos que:
Logo, vemos que os pontos enão têm um limite, já que seus limites laterais são diferentes.