UFCG – Lista 1 – Limite e Continuidade – 14f
Calcule os limites:
Passo 1
Fala povo, tudo certo?
Tá percebendo um negocinho diferente ali na parte do valor que precisamos tender no limite? Tem um sinal positivo ali. Você sabe o que isso significa?
Imagine o eixo como mostrado abaixo. O sinal de que está no valor que o precisa tender no limite indica que estamos nos aproximando daquele valor pelo lado DIRIEITO, ou seja, por valores que são MAIORES que .
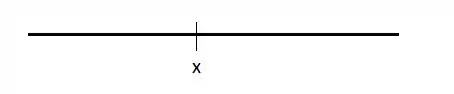
Agora que a gente entendeu o que significa aquele sinal de positivo ali, vamos seguir!!!
VEM COMIGOOO!
Passo 2
Essa parte agora é seguir o raciocínio parecido com o que temos sempre que fazer no primeiro passo em limites que é testar o valor que tem ali pra ver se vai dar alguma indeterminação.
No exercício, precisamos fazer , ou seja, precisamos fazer tender a por valores que são MAIORES que , por exemplo, .
Então vamos substituir isso no nosso limite e ver o que acontecerá?
Note que , ou seja, um valor muitooo pequeno!
Perceba então que quando fizermos
Percebe que deu um valor menor ainda?
Então você concorda comigo que podemos dizer que:
Passo 3
Passo 4
Logo, podemos aproximar nosso limite como sendo:
Note que o denominador é muitoooo pequeno, fazendo esse limite tender ao infinito, porém com sinal NEGATIVO!!
Bora que bora pra mais uma questão?