UFCG – Lista 1 – Limite e Continuidade – 14i
Calcule os limites:
Passo 1
Fala povo, tudo certo?
Tá percebendo um negocinho diferente ali na parte do valor que precisamos tender no limite? Tem um sinal positivo ali. Você sabe o que isso significa?
Imagine o eixo como mostrado abaixo. O sinal de que está no valor que o precisa tender no limite indica que estamos nos aproximando daquele valor pelo lado ESQUERDO, ou seja, por valores que são MENORES que .
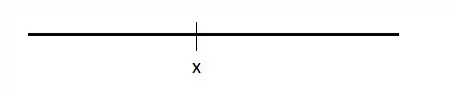
Agora que a gente entendeu o que significa aquele sinal de positivo ali, vamos seguir!!!
VEM COMIGOOO!
Passo 2
Essa parte agora é seguir o raciocínio parecido com o que temos sempre que fazer no primeiro passo em limites que é testar o valor que tem ali pra ver se vai dar alguma indeterminação.
No exercício, precisamos fazer , ou seja, precisamos fazer tender a por valores que são MENORES que , por exemplo, .
Mas ao invés de fazermos o , podemos pensar de uma outra forma que é mais prática e rápida pra desenvolver esse tipo de problemas.
VEM COMIGOO!
Passo 3
Uma outra forma de você avaliar o limite quando temos esses limites laterais (o sinal de mais ou menos no valor que o tende), é substituir o valor direto e aí sempre lembrar que ele é um valor que vai ser aproximado ou pela esquerda ou pela direita.
Note que isso gerará:
Mas aí beleza, o denominador deu um valor que vai tender a zero, logo temos um número divido por algo que é muitooooo pequeno e próximo de zero, ou seja, a resposta disso aí é INFINITO.
Mas precisamos agora analisar o sinal.
O denominador é . Porque eu coloquei esse “1”? Porque ele não é um 1 propriamente dito, né?
Se lembra que a gente obteve ele quando aproximamos , ou seja, quando colocamos um valor de um pouquinho de nada menor que .
Logo, temos que na nossa conta , o . Portanto, temos um valor no denominador que se aproxima de zero porééééééém, com um valor negativo!! Logo o infinito será também negativo uma vez que denominador é negativo e numerador é positivo.
Vamos pra mais uma questão!!!