Dadas as duas funções abaixo:
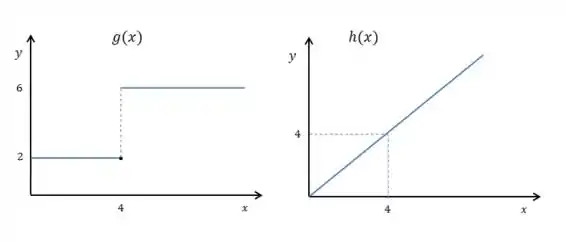
Calcule os limites laterais dados abaixo e verifique se o limite existe, comparando os limites laterais:
, , onde:
, , onde:
Passo 1
Bom, vamos primeiro escrever as leis das funções. Vamos começar por
A função é claramente uma função afim com equação:
Já que:
Já a função é uma função modular bem simples, descrita por:
Vamos calcular primeiro os limites laterais de por serem mais tranquilos:
Beleza, como você pode ver, eles são iguais.
A função vai gerar limites laterais diferentes:
E:
Show de bola?
Agora o vamos calcular os limites laterais de usando essas informações:
Usamos ali a propriedade do limite de um produto. Agora é só a gente pegar os valores que calculamos:
E agora:
De novo:
Show? Então, como os limites laterais são diferentes, o limite:
Não existe.
Passo 2
Precisamos lembrar que:
Beleza? Vamos usar os valores dos limites laterais do item anterior pra facilitar nossa vida.
Primeiro:
Já que:
Da mesma forma:
Como os limites laterais são diferentes, concluímos que:
Não existe.
Resposta
E o limite não existe.
E o limite não existe.