UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - UNICAMP - Lista 3 - Limite e Continuidade. Questão 21d
Prove as afirmações de limite:
se
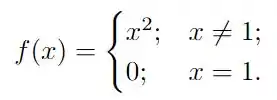
Passo 1
Ooopa! Tudo bem?
Temos que provar para cada alternativa nessa questão afirmações envolvendo limite, nesta em particular temos
se
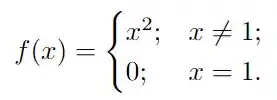
Note que aqui temos uma função com uma descontinuidade, mas como a descontinuidade é em apenas um ponto, pode ser que os limite exista, mas para garantir isso precisamos avaliar ambos os limites laterais
e
Vamos fazer isso!
Passo 2
Primeiro vamos avaliar o limite pela esquerda
Note que para qualquer valor que não seja , temos que , ou seja, como o limite não significa estarmos diretamente no valor , e sim nos aproximarmos dele, temos que
ou simplesmente
da mesma forma podemos garantir que
como temos que
o limite enunciado é válido! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!