UnB – Cálculo 1 – Lista de Exercícios 9 – Questão 5i
Para cada uma das funções abaixo, determine os pontos críticos, classifique-os como
máximos ou mínimos locais, quando for o caso, e determine os intervalos onde f é crescente e decrescente
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou te ajudar!
O problema nos deu essa função aqui
E pediu diversas coisas, vamos juntos decifrar o que significa cada uma dessas coisas?
“determine os pontos críticos”: pontos críticos são os pontos nos quais a derivada é igual a zero. Então aqui precisamos derivar e igualar a zero.
“classifique-os como máximos e mínimos locais”: um ponto de máximo será quando em torno do ponto crítico a derivada passou de positiva para negativa. E um ponto de mínimo acontece quando em torno do ponto, a derivada passa de um valor negativo para positivo
E por fim “determinar os intervalos onde é crescente e decrescente”: a função apresenta um comportamento crescente quando sua derivada é positiva, e decrescente quando é negativa
e é isso! Mas relaxa que vou fazer passo a passo com você!
Vamos começar?
Passo 2
Nossa função é
Para fazer a análise dos pontos críticos precisamos achar a derivada e igualar ela a zero:
Beleza? Temos apenas um ponto crítico: em , agora vamos substituir na função e descobrir a ordenada:
Então o ponto crítico é
Tudo bem até aqui?
Passo 3
Agora vamos analisar a derivada em torno desse ponto de :
- Para , mas maior do que zero (em zero a derivada não está definida):
- Para :
Então entre e a derivada assume valores negativos, então ali a função é decrescente
E à medida que aumenta, o termo , então temos que a derivada é positiva dali em diante, sendo a função crescente nesse intervalo
Beleza?
Passo 4
Agora vamos classificar esse ponto!
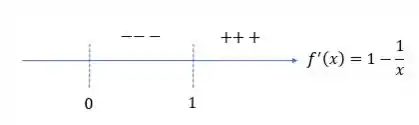
Obs.: embora a derivada esteja definida para , a função não está, então não faz sentido analisarmos antes do zero, beleza?
E é isso! Espero ter ajudado!