UERJ, Sem Campus, Cálculo I, Listas de C1 - IME UERJ - Aplicações das derivadas, Questão 15h
Calcule os pontos de inflexão (se existem) e estude a concavidade de:
(h)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar os pontos de inflexão da função e determinar também intervalos onde a função tem concavidade para cima ou concavidade para baixo. E quem poderá nos defender?
Ela mesmo. Isso porque existe um teorema que nos diz que se num intervalo , então a função é côncava para cima nesse intervalo. E se num intervalo , então a função é côncava para baixo nesse intervalo.
Então, o que nós vamos fazer é derivar a nossa função duas vezes e estudar o sinal dela, para e . Tá, e quando ? Aí teremos o famoso ponto de inflexão, que é quando a função muda de concavidade.
Vamos lá!
Passo 2
Nossa função é dada por:
Derivando ela em relação a , usando a regra do quociente, vamos obter:
Derivando mais uma vez, temos a segunda derivada:
Passo 3
Agora vamos ver o que acontece quando :
Como essa é uma função periódica, vamos analisar os intervalos que satisfaçam essa condição da desigualdade, para :
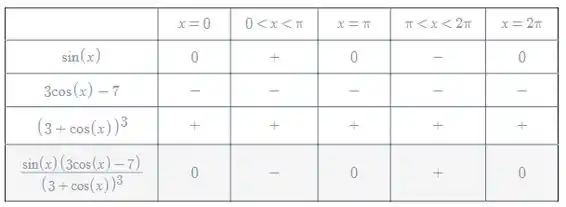
Repare, na última linha da tabela, que essa função só é positiva para Então, nossa função tem concavidade para cima no intervalo .
Da mesma forma, olhando na tabela, vamos que para . Então, nossa função tem concavidade para baixo no intervalo
Ultilizando a periodicidade, para um número inteiro , podemos extender essa análise para todo domínio da função, escrevendo:
Passo 4
Agora vamos verificar nossos pontos de inflexão fazendo :
Pra que esse produto seja verdadeiro, temos:
Para , teremos:
E para não temos solução real. Então, nossos pontos de inflexão ocorrem em ou , onde é um número inteiro.
Valeu, galera! Até a próxima! 😉