UERJ, Sem Campus, Cálculo I, Listas de C1 - IME UERJ - Aplicações das derivadas, Questão 14h
Usando a primeira derivada, determine os intervalos de crescimento e/ou decrescimento das seguintes funções:
(h)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar os intervalos onde a função cresce e/ou decresce.
Pra isso, vamos precisar fazer o famoso teste de crescimento e decrescimento, que basicamente consiste em verificar o sinal da derivada da função.
Isso porque se , em um intervalo , então a função é crescente nesse intervalo. E se , em um intervalo , então a função é decrescente nesse intervalo.
Então, vamos derivar a nossa função e fazer o estudo de sinal dela para verificar os intervalos de crescimento e decrescimento.
Vamos lá!
Passo 2
Nossa função é dada por:
Derivando ela em relação a , usando a regra do produto, vamos obter:
Agora vamos analisar o sinal de para verificar os intervalos onde a função é crescente ou decrescente.
Passo 3
Se olharmos os termos do produto, vamos ver que dependendo do valor de , a derivada será positiva (ou seja, maior que zero) ou negativa (menor que zero). Então, para montar o quadro de sinais, a gente começa achando os pontos em que cada termo será igual a zero, em outras palavras, vamos achar as raízes da equação. Fazendo:
Temos:
Agora vamos finalmente para o quadro de sinais. Vamos colocar em cima da tabela, em ordem crescente, todas as raízes dos termos e na primeira coluna colocamos os termos da derivada, a própria original e a nossa função .
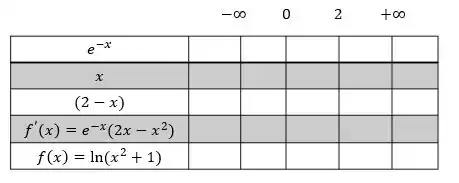
Então vamos preencher a tabela analisando os intervalos onde cada termo é negativo ou positivo, na primeira e na segunda linha. Na linha da derivada, a gente preenche fazendo a multiplicação dos sinais de cada termo.
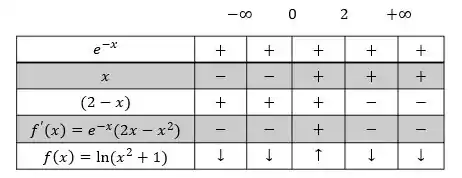
As setinhas para cima indicam onde a derivada é positiva e consequentemente, os intervalos de crescimento da função. Assim como as setinhas para baixo, indicam onde a função decresce. Representanto esses intervalos, vamos ter:
Valeu, galera! Até a próxima! 😉