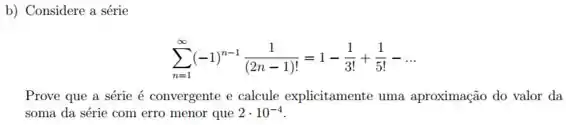
Passo 1
Trata-se de uma série alternada, então devemos usar o critério de Leibniz. Assim vamos ver se a sequência é decrescente e seu termo geral tende a zero.
Primeiro critério atendido.
Segundo critério também atendido, logo a série converge absolutamente.
Passo 2
Vamos agora aproximar a série para que . Para as séries alternadas nós temos:
E o melhor, isso vale sempre! Então basta que encontremos um valor de tal que:
Agora ficou mais simples, não é mesmo?
Passo 3
Vamos enão calcular o valor desse :
Testando valores para essa desigualdade vemos que:
Assim, podemos aproximar a série para três termos. Então:
Resposta
Exercícios de Livros Relacionados
2-20. Teste a série quanto a convergência ou divergência. ∑ n = 1 ∞ - 1 n n 2 n + 3
Para quais valores de p cada série é convergente? ∑ n = 1 ∞ - 1 n n + p
Mostre que a série é convergente. Quantos termos da série precisamos somar para encontrar a soma parcial com a precisão indicada? |erro| ≤ 0,0001 ∑ n = 1 ∞ - 1 n n 5 n
Teste a série quanto a convergência ou divergência. ∑ n = 1 ∞ - 1 n + 1 n + 1
Teste a série para convergência ou divergência.6- ∑ n = 1 ∞ - 1 n - 1 3 n - 1