Determine se a série
Converge ou diverge no seguinte caso:
Passo 1
Bom, a gente sempre deve fazer o teste da divergência antes de tentar qualquer outro teste (a não ser que a série envolva um fatorial ou seja muito complicado de calcular o limite), porque se o cara for divergente, a gente já mata a questão, ok? Você lembra o que diz o teste da divergência?
Relaxa, nada mais é que calcular o limite do termo geral da série, quando . Se esse limite for diferente de zero, a série diverge, e se ele for igual a zero, nada podemos concluir. Então bora fazer esse teste:
Confesso que esse limite não é um dos mais fáceis, mas repara que temos uma quantidade crescendo muito no denominador e uma outra quantidade sendo ou . Todo esse termo está cada vez menor, indo pra zero. Você pode usar o Teorema do Confronto pra ver isso.
Na real, como estamos com uma série alternada, você não precisa se preocupar muito em fazer o teste da divergência.
Então faremos outro teste!
Passo 2
Cara, sempre que você se deparar com uma série alternada, faça o teste da série alternada, é ele que tem que vir na sua mente! Se você tem uma série , esse teste pede que respeite as seguintes condições para que a nossa série seja convergente:
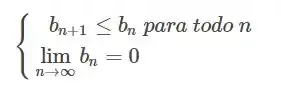
Ou seja, o termo que acompanha o tem que ser DECRESCENTE e o limite ir pra zero.
Passo 3
Identificando nosso termo :
Pensa comigo: é uma função crescente, ou seja:
Isso quer dizer que:
Em outros termos:
Shooooow, nosso é decrescente!
Passo 4
Bora calcular o limite dele!
Maneiro demaaais! Então nossa série converge!
Resposta
A série converge.