Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Série alternada

Ver Teoria
Exercício 221234567891011121314151617181920212324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Determine se a série ∑ k = 1 ∞ x k converge ou diverge nos casos x k = a k , b k , c k , d k ,   e k   e   f k onde:

a k = k 2 + 3 k 2 k + 1 2

b k = 2 k + 6 k 3 k + 3 2 k

c k = - 1 k + 1   k k + 1

d k = - 1 k k ln ⁡ k - 1

e k = k - 1 k   4 k

f k = k k + 1 k 2

Passo 1

Vamos começar com x k = a k

∑ k = 1 ∞ k 2 + 3 k 2 k + 1

Vamos começar usando o teste da comparação no limite, que diz que dadas duas séries ∑ a n e ∑ b n , se ao tomarmos o limite da razão delas lim k → ∞ ⁡ a n b n = C > 0 , então ou ambas divergem, ou ambas convergem. Vamos ajeitar nosso termo geral:

k 2 + 3 k 2 k + 1 2 = k 2 + 3 k 2 ( k 2 + 2 k + 1 ) = k 2 + 3 k 4 + 2 k 3 + k 2

Então:

a n = k 2 + 3 k 4 + 2 k 3 + k 2

Agora, vamos escolher b n como o cara maior grau no numerador, divido pelo cara de maior grau no denominador:

b n = k 2 k 4 = 1 k 2

Ficamos com:

lim k → ∞ ⁡ k 2 + 3 k 4 + 2 k 3 + k 2 1 k 2 = lim k → ∞ ⁡ k 2 + 3 k 4 + 2 k 3 + k 2 k 2 = lim k → ∞ ⁡ k 2 + 3 k 2 + 2 k + 1

Dividindo o numerador e o denominador por k 2 :

lim k → ∞ ⁡ 1 + 3 k 2 1 + 2 k + 1 k 2 = 1 > 0

Logo, o que acontece com ∑ 1 / k 2 , acontece com a nossa série também.

Portanto, como   ∑ 1 / k 2 é convergente (p-série com p > 1 ) nossa série é convergente.

Passo 2

Para x k = b k :

∑ k = 1 ∞ 2 k + 6 k 3 k + 3 2 k

Primeiro, vamos arrumar esse termo geral:

2 k + 6 k 3 k + 3 2 k = 2 k + 2 k 3 k 3 k + 3 2 k = 2 k 1 + 3 k 3 k 1 + 3 k = 2 3 k

Nooooooossa! Repara que isso é uma série geométrica! Lembra?

∑ r k r < 1 ,     c o n v e r g e n t e r > 1 ,     d i v e r g e n t e

Nesse caso, 2 3 < 1 . Logo, a série é convergente.

Passo 3

Para x k = c k :

∑ k = 1 ∞ - 1 k + 1 k k + 1

Aqui, vamos usar o teste da série alternada, que pede que respeitemos duas condições:

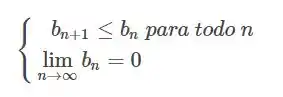
Ou seja, o termo que acompanha o ( - 1 ) precisa ser decrescente e o seu limite precisa ser 0 .

No nosso caso,

b n = k k + 1

Ele é decrescente, pois k cresce menos rápido que k + 1 , que o está dividindo. Vamos ver como fica esse limite:

lim k → ∞ ⁡ k k + 1

Usando L’Hôpital:

lim k → ∞ ⁡ 1 2 k 1 = lim k → ∞ ⁡ 1 2 k = 0

Então, a série é convergente.

Passo 4

Para x k = d k

∑ k = 1 ∞ - 1 k k l n k - 1

Vamos usar o teste da série alternada, que pede que respeitemos duas condições:

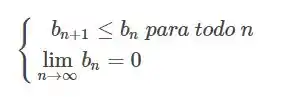
Onde b n é o cara que acompanha o ( - 1 ) , que no nosso caso é b n = 1 k l n k - 1

Dado que:

k l n k - 1 < k + 1 ln ⁡ k + 1 - 1

Temos que b n + 1 ≤ b n

Calculando seu limite:

lim k → ∞ ⁡ 1 k l n k - 1 = 0

Portanto, a série é convergente.

Passo 5

Para x k = e k

∑ k = 1 ∞ k - 1 k 4 k

Vamos usar o teste da razão, que diz

Então, calculando

a n = k - 1 k 4 k

a n + 1 = k + 1 - 1 k + 1 4 k + 1 = k k + 1 4 k + 1

lim k → ∞ ⁡ k k + 1 4 k + 1 k - 1 k 4 k = lim k → ∞ ⁡ k 4 k k - 1 k k + 1 4 k + 1 = lim k → ∞ ⁡ k 2 ( k - 1 ) k + 1 4 = lim k → ∞ ⁡ k 2 4 k 2 - 4

lim k → ∞ ⁡ k 2 4 k 2 - 4 = lim k → ∞ ⁡ 1 4 - 4 k 2 = 1 4

Então, a série é convergente.

Passo 6

Para x k = f k

∑ k = 1 ∞ k k + 1 k 2

Vamos usar o teste da raiz, que diz o seguinte:

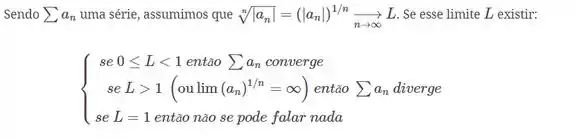
Então vamos lá:

lim k → ∞ ⁡ k k + 1 k 2 k = lim k → ∞ ⁡ k k + 1 k = lim k → ∞ ⁡ k + 1 k - k = lim k → ∞ ⁡ 1 + 1 k - k

= lim k → ∞ ⁡ 1 + 1 k k - 1 = lim k → ∞ ⁡ 1 + 1 k k - 1 = e - 1 = 1 e

Sabendo que 0 < 1 e < 1 , a série é convergente.

Resposta

x k = a k → convergente

x k = b k → convergente

x k = c k → convergente

x k = d k → convergente

x k = e k → divergente

x k = f k → convergente

Exercícios de Livros Relacionados

2-20. Teste a série quanto a convergência ou divergência. ∑ n = 1 ∞ - 1 n n 2 n + 3
Para quais valores de p cada série é convergente? ∑ n = 1 ∞ - 1 n n + p
Mostre que a série é convergente. Quantos termos da série precisamos somar para encontrar a soma parcial com a precisão indicada? |erro| ≤ 0,0001 ∑ n = 1 ∞ - 1 n n 5 n
Teste a série quanto a convergência ou divergência. ∑ n = 1 ∞ - 1 n + 1 n + 1
Teste a série para convergência ou divergência.6- ∑ n = 1 ∞ - 1 n - 1 3 n - 1