Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Derivação Implícita

Ver Teoria
Exercício 117123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

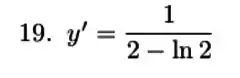
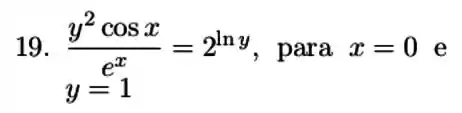
Passo 1

Vamos derivar essa função implícita aí!

y 2 cos ⁡ x e x ' = 2 ln ⁡ y '

Lembrando, ao derivar as funções de y vai aparecer um y ' , pela Regra da Cadeia, que é justamente o que procuramos nessa questão.

y 2 cos ⁡ x ' e x - y 2 cos ⁡ x e x ' e x 2 = ln ⁡ 2 2 ln ⁡ y ' ln ⁡ y '

y 2 cos ⁡ x ' + y 2 ' cos ⁡ x e x - y 2 cos ⁡ x e x e 2 x = ln ⁡ 2 2 ln ⁡ y y ' y

y 2 - sen ⁡ x + 2 y y ' cos ⁡ x e x - y 2 cos ⁡ x e x e 2 x = ln ⁡ 2 2 ln ⁡ y y ' y

Está derivado! Eu sei que ficou bem feia essa expressão, mas agora tudo se resume a pegar isso e aplicar os valores de x e y pedidos:

Passo 2

Aplicando

x = 0       ;       y = 1

Teremos:

1 2 - sen ⁡ 0 + 2 1 y ' cos ⁡ 0 e 0 - 1 2 cos ⁡ 0 e 0 e 2 0 = ln ⁡ 2 2 ln ⁡ 1 y ' 1

0 + 2 y ' 1 1 - 1 1 1 = ln ⁡ 2 2 0 y '

2 y ' - 1 = ln ⁡ 2 1 y '

y ' 2 - ln ⁡ 2 = 1

y ' = 1 2 - ln ⁡ 2

Resposta

Exercícios de Livros Relacionados

Nos Exercicios de 1 a 28, ache d y d x por derivação implícita7. x + y = 4
Exercício de Livro
Encontre d y // d x derivando implicitamente.x^2 + y^3 = 1
Considere y como variável independente e x como variável dependente e use a derivação implícita para encontrar d x / d y . y sec ⁡ x = xt gy
a) Encontre y ' derivando implicitamente.b) Resolva a equação explicitamente isolando y e derive para obter y ' em função de x .c) Verifique que sua soluções das partes (a) e (b) são consistentes, sub